Rotation and Torque Workshop
The purpose of this open-‐ended experiment is to explore the concepts of rotational kinematics and torque.
You will design and conduct experiments to apply Newton’s second law to rotating systems, Newton’s first law to a system in equilibrium, and you will practice calculating rotational quantities.
Hoveroverthese
- Using the pulley and photogate system, attach two different masses to a string to create
an Atwood’s machine, as shown to the right. Choose masses that have
relatively close quantities. Set the photogate to the correct settings for
measuring the motion
of the pulley – the mode should read “photogate timing,” with “photogate mode”
measuring the “pulley” and “outside edge” for 25 events.
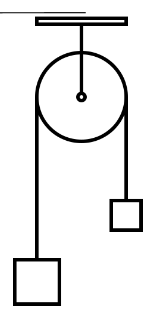
- Release the system from rest and collect data on its motion. As we saw last time, the graph will display tangential velocity vs. time. We will assume the friction acting on the pulley in negligible, as is the mass of the string.
- Use your data to calculate the following showing all work and using correct units:
- Tangential acceleration of the system (how did you find this?).
- Angular acceleration of the system (circumference of inner groove = 0.150 m).
- Sum of the torques acting on the pulley (neglecting F f ).
Previously we assumed negligible friction on the pulley but we know there must be some degree of friction or the pulley would spin forever. Remove the masses and string.
- Spin the pulley and devise a procedure for estimating the frictional torque acting on it (you may
use the photogate for this). Use your calculated value for the moment of inertia
of the pulley from your Rotational Acceleration measurements.
- Estimate the number of revolutions from start to finish. Show your calculations below with appropriate formulas and correct units.
- Balance a meter stick on a fulcrum using two different masses attached to two different positions, as shown below. Test to make sure the system is well balanced. Sketch a free body diagram and determine the moment of inertia of the system, the sum of the torques, and the force of the fulcrum on the meter stick. Show your calculations with correct units.
- Suppose you were to remove one of the masses (choose which one). Calculate the following showing
all work with correct units:
- Moment of inertia of the system.
- Net torque on the system.
- Angular acceleration of the system.
- Tangential acceleration at the tip of the meter stick.
- Rotational velocity after the system has rotated 90°.
Hovering over these bubbles will make a footnote pop up. Gray footnotes are citations and links to outside references.
Blue footnotes are discussions of general physics material that would break up the flow of explanation to include directly. These can be important subtleties, advanced material, historical asides, hints for questions, etc.
Yellow footnotes are details about experimental procedure or analysis. These can be reminders about how to use equipment, explanations of how to get good results, or clarifications on details of frequent confusion.
Value is from NOAA for Latitude: 40.91597332879679, Longitude: -73.12491620370486, MSL Height: 41.0 Predicted gravity: 980269 +/- 2 milligals where a "gal" is a centimeter per second squared