The purpose of these simulations is to explore the concepts of thermal energy transfer and conservation, and the relationships among pressure, volume, temperature, energy, and work. You will modify and observe two sets of interactive simulations to apply the ideal gas law and the first law of thermodynamics.

Resources

• Physics Aviary simulation on “Gas in a Box”
• WebAssign Simulations

Thermodynamics refers to the description of macroscopic processes resulting from the effects of heat, other forms of energy, and work. State variables refer to the quantities that macroscopically describe the state of a system, such as volume, temperature, and pressure. The microscopic state of the system involves the details of motion of atoms or molecules within the system; this motion is described by kinetic theory, which assumes gas molecules are relatively far apart, move in random motion with a distribution of speeds, collide elastically, and exert negligible forces on each other in a closed system. There are four principle laws of thermodynamics, which help us comprehend and predict macroscopic properties. Our primary focus is the first law of thermodynamics, which states the change in internal energy \( \Delta E_{int} \)of a closed system is equal to the energy added to the system \( Q \) plus the work done on the system \( W \) by its surroundings: $$ \Delta E_{int} = Q + W $$ As a gas expands, it does positive work on its surroundings; as it contracts, it does negative work on its surroundings and positive work is done on the system. The internal energy of a system is directly related to temperature: $$ E_{int} = \frac{3}{2} nRT $$ $$ \Delta E_{int} = \frac{3}{2} nR \Delta T $$ The simulations, accessed through several websites, will explore relationships among state variables, as well as the first law of thermodynamics.

Procedure, Questions & Calculations

1. You can choose the gas type in your box by clicking on the name of the noble gas. Move the piston to choose the volume you would like to add then click on the words “movable piston” so that it changes to “fixed position.” This will constrain the volume.
2. Record the values for number of moles, temperature, and pressure. Make sure the system is uninsulated and then change the environment – this should either add or remove heat to the system and change the temperature. Record the values for number of moles, temperature, and pressure. Change the environment three more times, adding or removing heat, for a total of five sets of values.
3. Using one of the online plotting tools , demonstrate that the behavior of the gas molecules obeys Gay-­‐Lussac’s Law by creating a pressure-­‐temperature graph: $$ \frac{P}{ T} = constant $$ Record your slope (constant) with the appropriate units.
4. Determine the volume of the gas from the ideal gas law: \( PV = nRT \) Use your slope value from the previous graph to best approximate \( \frac{P}{T} \). Calculate the volume using \( R = 8.314\) J/(mol·∙K). Compare the volume you calculated from this measurement with your result from measuring the length of the box using the ruler in the simulation.
5. Check that the values provided by the simulation satisfy the following equation for the average speed of an atom or molecule, where Boltzmann’s constant \( k = 1.38 x 10^{‐23}\) J/K. The variable m is the mass of one atom of the noble gas. Note that average speed is calculated differently from root mean square velocity. $$ \bar{v} ≈ 1.60\sqrt \frac{kT}{m} $$
6. Repeat steps 2-­‐5 for a second noble gas. How does the mass of the gas affect your results?

Now that you are familiar with the general relationships among state variables, we will explore situations involving isobaric (constant pressure), isochoric (constant volume), isothermal (constant temperature), and cyclic processes. Open the simulation on Isobaric vs. Isochoric Heating

I. Procedure & Questions – Isobaric Process

1. In this process, pressure and number of molecules remains constant, while volume and temperature change. This relationship is defined by Charles’s law: V T = constant
2. In the simulation, the isobaric process is the one that goes from i -> f’. You can adjust the initial and final temperature using the sliders at the bottom of the screen.
3. Considering an isobaric process in which the temperature increases, what happens to the volume? Explain briefly in terms of kinetic theory.
4. As the temperature increases, does the system do positive, negative, or zero work on its surroundings?
5. As the temperature increases, is \( Q \) positive, negative, or zero?
6. Does the internal energy of the system increase, decrease, or remain the same as the temperature increases?

II. Procedure II & Questions – Isochoric Process

1. In an isochoric process, volume and number of molecules remains constant, while pressure and temperature change. This direct relationship is defined by Gay-­‐Lussac’s law: $$ \frac{P}{T} = constant $$
2. In the simulation, the isobaric process is the one that goes from i -> f. You can adjust the initial and final temperature using the sliders at the bottom of the screen.
3. As the temperature increases, does the system do positive, negative, or zero work on its surroundings?
4. As the temperature increases, is Q positive, negative, or zero?
5. Does the internal energy of the system increase, decrease, or remain the same as the temperature increases?

III. Procedure III & Questions – Isothermal Process

1. Open the simulation on Isothermal Compression In this process, temperature and number of molecules remains constant, while pressure and volume change. This inverse relationship is defined by Boyle’s law: $$ PV = constant $$
2. As the volume increases, what happens to the pressure? Explain briefly in terms of kinetic theory.
3. As the volume increases, does the system do positive, negative, or zero work on its surroundings?
4. As the volume increases, is \( Q \) positive, negative, or zero?
5. Does the internal energy of the system increase, decrease, or remain the same as the volume increases?

IV. Procedure IV & Questions – Cyclic Process

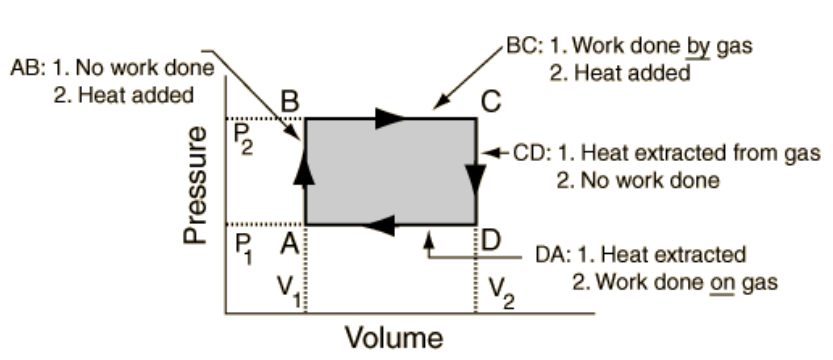
1. Consider the rectangle below representing a cyclic process for one mole of an ideal gas with its top left corner (point B) representing a volume of \( 10dm^3 \) and pressure \( 120kPa\). The bottom right corner (point D) represents a volume of \(40 dm^3 \) and pressure \( 30kPa\) . The process starts at the top left corner. In analyzing the energy changes during this cyclic process, you will need to know the temperatures of the system at the corners of the rectangle.
2. Calculate the temperature at each corner of the rectangle (TA, TB, TC, TD), labeling according to the diagram below. State variables must be in the correct units: \( 1 dm^3 = (0.1 m)^3 \), pressure must be in Pa, and \( R = 8.314 \) J/mol·∙K. Remember, after calculating the first temperature, you may use simple ratios to find the temperature at the other points.
3. What is the change in internal energy from point B to point D?
4. How much heat was added or removed from point B to point D?
5. What is the change in internal energy for one complete cycle

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

PHY121/122 Plotting Tool

PHY131/132 Plotting Tool