The purpose of this lab is to explore how the position of the object affects the appearance, orientation, and size of real and virtual images produced by mirrors and lenses. You will examine the relationship among object distance, image distance, focal length, and magnification in real images produced by concave mirrors and converging lenses. You will use the ray diagrams for thin lenses and convex mirrors to sketch the produced image.

• Dynamics system track
• Optics expansion kit
• Mirror set
• Ruler
• Record data in this (draft) Google Sheets data table

Curved Mirrors

Images formed by a curved mirror can be either real or virtual, magnified (bigger than the object) or reduced (smaller than the object), upright (same orientation as the object) or inverted. Real images can be viewed directly by eye or they can be projected and viewed on a screen. Virtual images cannot be projected to a screen.

In our lab the shape of the mirror fits to a sphere of radius R. The size of the mirror is much less than R. (There are other curved mirrors, in parabolic, elliptical and other shapes. Most of the time, if the mirror is small enough, its shape can be approximated by a sphere.) If the light is reflected from the inner surface of the sphere the mirror is called a converging or concave mirror. A mirror that reflects light from its outer surface is called a diverging or convex mirror. Here you will study the images formed by a concave mirror.

The mirror equation for any curved mirror is $$\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}$$

Where, \(d_o\) is the distance from the object to the mirror, \(d_i\) is the distance from the image to the mirror and \(f\) is the focal length, which represents half of the radius of curvature of the mirror \(f=R/2 \). In order to use equation (1) you need to keep in mind the sign conventions, which are summarized as follows:

• \(d_o\) (\(d_i\)) is positive if the object (image) is in front of the mirror, real image.
• \(d_o\) (\(d_i\)) is negative if the object (image) is in back of the mirror, virtual image.
• \(f\) is positive if the center of curvature \(R\) is in front of the mirror, concave mirror.
• \(f\) is negative if the center of curvature \(R\) is in back of the mirror, convex mirror.

The magnification \(M\) for a mirror is given by $$m=\frac{h_i}{h_o} = -\frac{d_i}{d_o}$$ \(M\) is positive if the image is upright, and negative if the image is inverted.

PROCEDURE

Click here for an image of the Mirror set-up

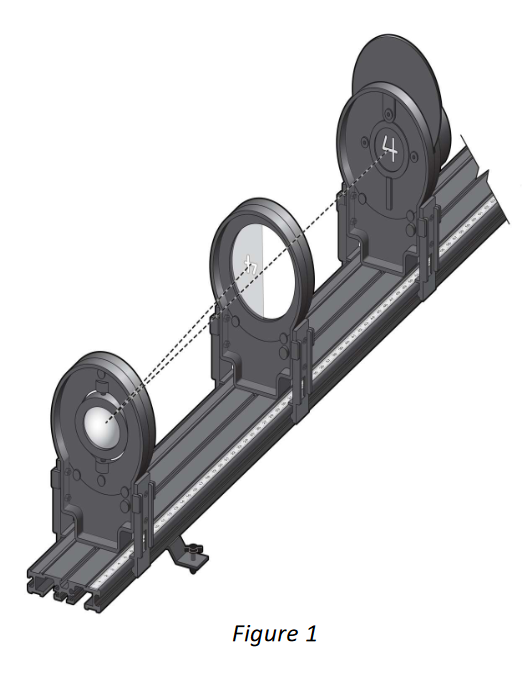
1. Set up the light source and concave mirror to project a clear image on the half screen.
   1. Attach the light source assembly from the Optics Expansion Kit to the Vernier track. Position it so that the pointer in the base is at the 10cm mark and the light source faces the other end of the track. Switch on the light.
   2. Place the adjustable mirror (nominal focal length is 20cm) near the other end of the track so that it faces the light source. Attach the half screen to the track between the light source and the mirror.
   3. Turn the light source wheel until the number “4” is visible in the opening. This will be your “object” at position 10cm.
   4. Adjust the position of the screen until the image of the “4” on the screen is in focus (see Figure 1). You may need to adjust the angle of the mirror in its holder so that the image projected by the mirror shows on the screen. One approach to obtain the sharpest image, once you think you have it, is to move the screen in either direction until the image begins to blur, then move it back until it again appears sharp.
2. Describe the size, shape, and orientation of the image.
3. Now, move the mirror to the 60cm mark, then move the half screen until you can see a sharp image of the “4” on it. Record the distance between the light source and the mirror as “object distance” \(d_o\) and the distance between the mirror and the screen as “image distance” \(d_i\) in Table 1. Estimate their uncertainties.
4. Measure the height of the object \(h_o\) and the image on the screen \(h_i\). Record these values in Table 1 and estimate their uncertainties.

Analysis

Evaluate the data:

1. Complete the data table with the measured data.
2. On graph paper below make a drawing – to scale (1 square = 2cm in the horizontal direction, but 1 square = 0.25 cm in the vertical direction) – containing object and image arrows and the mirror with object and image distance and the nominal focal length of 20 cm. Reconstruct the image with the principal rays.
3. Use equation (1) to calculate the focal length \(f\) of the lens and its error from your measured \(d_o\) and \(d_i\) values. Hint: to calculate the error of \(f\), use the fact that the reciprocals \(1/d_o\), \(1/d_i\)and \(1/f\) have the same relative errors as \(d_i\) , \(d_o\) and \(f\), and propagate the absolute errors of the reciprocals according to Uncertainty/Error Manual.
4. Compare your obtained value of \(f\) with the nominal value of 20 cm. Are they consistent?
5. Find the magnification from the measured heights of the image and object using equation (2). Calculate the error in the measured magnification from the errors in \(h_i\) and \(h_o\) using the relative errors added in quadrature, ie, $$\frac{\delta M}{M} = \sqrt{{(\frac{\delta h_i}{h_i})}^2 + {(\frac{\delta h_o}{h_o})}^2}$$
6. Calculate the magnification from the measured image and object distances using equation (2) and find its error by using same previous equation. $$\frac{\delta M}{M} = \sqrt{{(\frac{\delta d_i}{d_i})}^2 + {(\frac{\delta d_o}{d_o})}^2}$$

   Are the two values obtained for the magnification consistent with each other?

Thin Lenses

In this part you will study images formed by a thin lens. Similar to mirrors, the image formed by a lens can be either real or virtual, magnified or reduced, upright or inverted. The thin-lens equation is: $$\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}$$ Where, \(d_o\) is the distance from the object to the mirror, \(d_i\) is the distance from the image to the mirror and \(f\) is the focal length. (The lens is thin if its thickness is much less than the focal length.)

The sign convention for lenses is different from mirrors, due to the fact that for lenses the light passes through the lens. The front of the lens is where the incident light hits the lens. The light is refracted inside the lens and leaves it from the back.

A lens that collects the light of a parallel light beam into a converging beam focused to a sharp spot is called converging lens. A lens that takes a converging beam and turns it into a parallel beam is called diverging lens. A converging lens is thicker in the center that in the edge and at least one of its surfaces is convex (the center of curvature is on the side of the refracting medium).

Diverging lenses are thinner in the center than at the edge and at least one of the surfaces is concave (the center of curvature is on the opposite side of the refracting medium).

• \(d_o\) (\(d_i\)) is positive if the object (image) is in front (back) of the lens, real image.
• \(d_i\) is negative if the image is in back (front) of the lens, virtual image.
• \(f\) is positive for converging lenses.
• \(f\) is negative diverging lenses.

The magnification \(M\) is given by $$m=\frac{h_i}{h_o} = -\frac{d_i}{d_o}$$ M is positive if the image is upright and negative if the image is inverted.

PROCEDURE: Converging Lenses

Click here for an image of the lens set-up

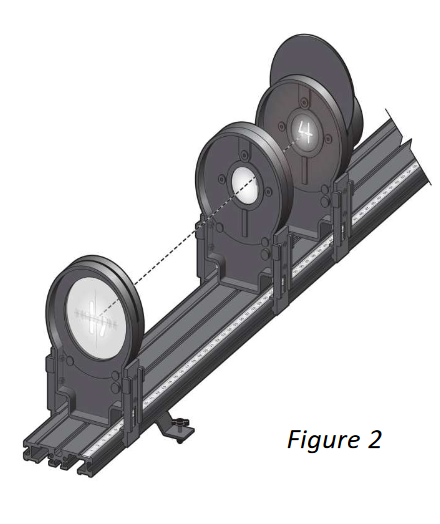
1. Set up the light source and lens to project a clear image on the screen.
   1. Attach the light source assembly from the Optics Expansion Kit to the Vernier track. Position it so that the pointer in the base is at the 10 cm mark and the light source faces the other end of the track.
   2. Place the 10 cm converging (double convex) lens on the track at the 35 cm mark. This sets up an object distance of 25cm.
   3. Attach the screen to the track and position it so that light from the light source passes through the lens and strikes the screen.
   4. Turn the light source wheel until the number “4” is visible in the opening. This will be your “object” for this investigation.
   5. Adjust the position of the screen until the image of the “4” on the screen is in focus. One approach to obtain the sharpest image, once you think you have it, is to move the screen until the image begins to blur, then move it back until it again appears sharp.
2. Describe the size, shape, and orientation of the image.
3. Record the distance between the light source and the lens as “object distance” (\(d_o\)) and the distance between the lens and the screen as “image distance” (\(d_i\)) on Table 2. Estimate their uncertainties.
4. Measure the height of the object (\(h_o\)) and the image on the screen (\(h_i\)). Record these values on Table 2.
5. Repeat the procedure with object distance of 20cm, 15cm and 13cm.

Analysis

Evaluate the data:

1. Complete Table 2 with the measured data. For the errors of the object distance and image distance use \(\delta d_o = \delta d_i = 0.5\)cm. The errors of the reciprocals are \(\delta 1/d_o = \delta d_o/d_o^2\) and \(\delta 1/d_i = \delta d_i/d_i^2\).
2. On the graph paper below make a graph of \(1/d_i\) on the horizontal (x) axis and \(1/d_o\) on the vertical (y) axis. Indicate the error bars. Draw a straight line through the data points so that it intercepts the “y” axis (at \(x=0\)). According to Eq. (3), how is the focal length related to the value of y at the intercept? What is the focal length and its error?
3. Compare your obtained value of \(f\) with the nominal value of 10 cm. Are they consistent?
4. For each object distance find the magnification from the measured heights of the image and object using equation (4). Calculate the error in the measured magnification from the errors in \(h_i\) and \(h_o\) using the relative errors added in quadrature, ie, $$\frac{\delta M}{M} = \sqrt{{(\frac{\delta h_i}{h_i})}^2 + {(\frac{\delta h_o}{h_o})}^2}$$
5. Calculate the magnification from the measured image and object distances using equation (4) and find its error by using same previous equation, $$\frac{\delta M}{M} = \sqrt{{(\frac{\delta d_i}{d_i})}^2 + {(\frac{\delta d_o}{d_o})}^2}$$

   Are the two values obtained for the magnification consistent with each other?

More Observations

6. Take a piece of paper and cover the upper half of the converging lens. What do you observe on the screen:
   1. Half of the image corresponding to the lower half part of object
   2. Half of the image corresponding to the upper half part of object
   3. Complete image but at half intensity
   4. No image at all.
   Explain your observation.
7. Switch off the light at the object. Remove the screen, position your eye approximately 30cm from the lens holder and look through the lens. Change the object distance by moving the lens closer to the source. Note what happens to the size of the image and the orientation as the object distance decreases.

Is the image always inverted? Does it become upright at some point? Explain.

Is the image always real? Does it become virtual at some point? Explain.

PROCEDURE: Diverging Lenses

Diverging Lens (Virtual images)

1. Switch on the light for the object. From the previous set up (Figure 2), place the 15 cm diverging (double concave) lens on the track, at the 50 cm mark.
2. Adjust the position of the screen until the image of the “4” on the screen is in focus (sharp image). Could you find any image on the screen? If the answer is NO, explain the reason why an image cannot be projected on the screen when using a diverging lens.
3. Position your eye approximately 30 cm from the lens holder and look through the lens. Describe the size, shape, and orientation of the image.
4. Change the object distance by moving the lens closer to the source. Note what happens to the size of the image and the orientation as the object distance decreases (do not need to use the screen, only position your eye a certain distance from the lens holder and look through the lens).

Is the image always upright or inverted? Does it change from upright to inverted at some point?

How is the size of the image changing?

Does at any point (moving the lens further or closer to the object) the size of the image become larger than the size of the object?

Answer the following question: According to what you have studied in this lab, is a magnify glass made of a converging or a diverging lens? Why?

1/23/2017 .docx file available from Laszlo Mihaly

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

Ray Tracing Diagram Paper