Bragg Scattering

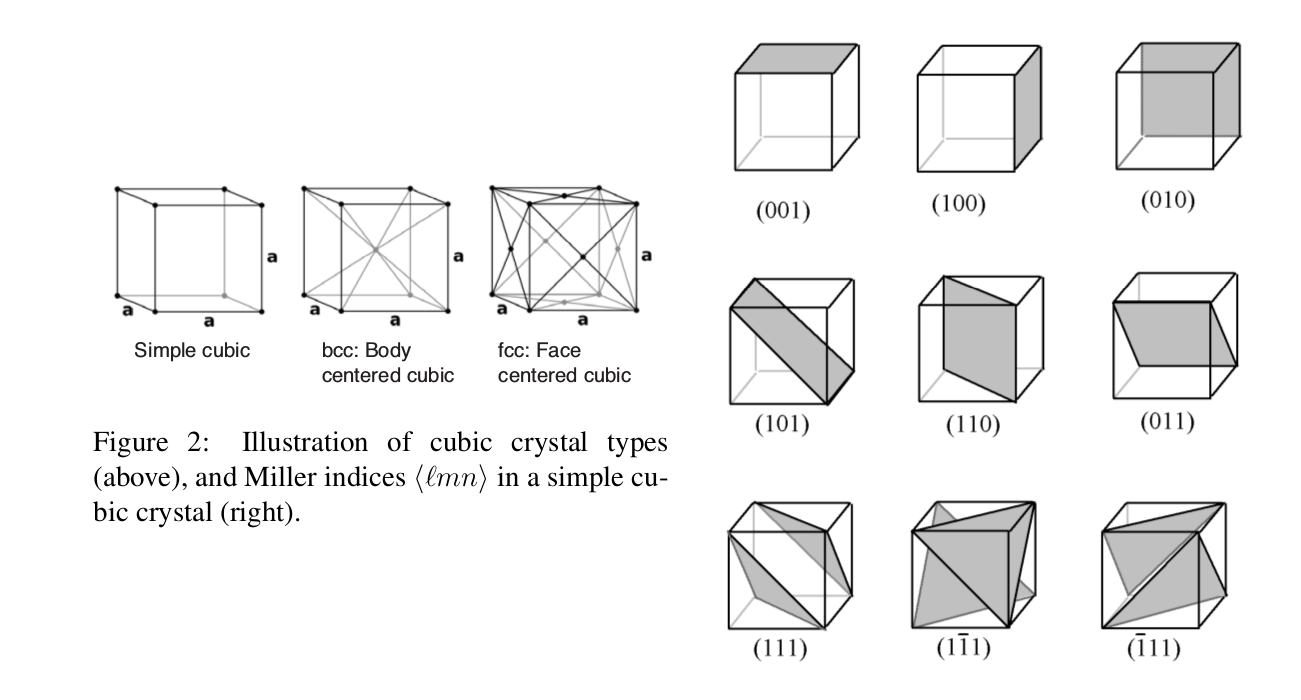
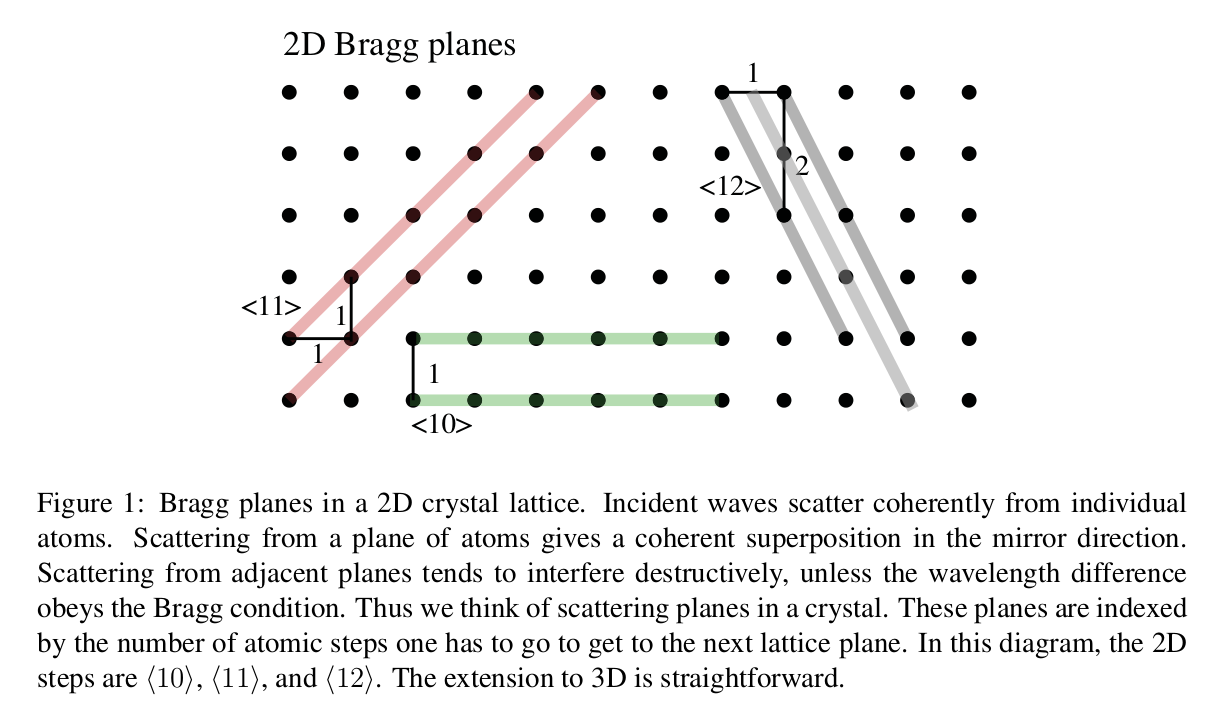
In this experiment, we will study the scattering of microwaves from a “crystal” made up of ball bearings embedded in styrofoam. We will find diffraction maxima having the same form as those encountered in Bragg scattering of X-rays from crystal lattices. Fig. 1 shows a 2D version, but our “crystal” is 3D, as in Fig. 2. In the case when all atoms are in a simple cubic form with lattice constant $a$, the distance between planes is

$d=\frac{a}{\sqrt{l^{2}+m^{2}+n^{2}}}$

where $l$, $m$, $n$ are integers with no common divisor, called the Miller indices. The different scattering planes of a crystal are labeled by their Miller indices as $\langle lmn \rangle$.

Microwaves are electromagnetic waves (light) with wavelengths in the range 0.001 to 0.3 m, shorter than radio waves and longer than infrared. Ordinary microwave ovens usually use 2.45 GHz, wavelength $\lambda$ = 0.122 meters. Our microwave generators make somewhat shorter wavelengths (you will measure this). The source in an ordinary microwave oven is a “cavity magnetron.” In the lab, our source is a “klystron.” This uses resonant cavities, and an electron beam that amplifies the microwave energy in the cavities.

1. Set up the microwave transmitter and receiver on a meter stick so that the horn antennas face each other. Turn on the transmitter and turn up the receiver sensitivity to about half-scale. The older equipment has transmitters that should be tuned to a point that gives best response at the receiver. As you perform the experiment, periodically check the tuning, which can tend to drift. Be careful with the apparatus, as the klystron can get quite hot. In the newer equipment (which does not necessarily function better than the older equipment) the klystrons are hidden and tuning is not an option. You do not need to worry about danger from the microwaves themselves. Notice what happens to the receiver response when you put your hand between the two horn antennas.
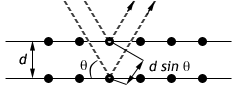
2. The transmitter/receiver system defines a low-grade optical cavity. When you have an odd number of half-waves between the two ($\frac{n\lambda}{2}$ with $n$ odd), you will see intensity minima in the receiver. Use this to determine the wavelength, by slowly moving the receiver straight out along the meter stick, measuring the distances of the successive intensity minima. Take readings over a wide range of distances to minimize the error.
3. Now place the transmitter and receiver on the arms of the goniometer. Systematically look for Bragg scattering from the “crystal” planes, seeking in particular the $\langle 100 \rangle$ , $\langle 110 \rangle$ , and $\langle 111 \rangle$ planes from a a simple cubic lattice. In each case, test the Bragg formula $2d\sin\theta =n\lambda$. The procedure you will need to follow is to align the scattering planes so that the incident and scattered angle to the planes are both $\theta$ where the value of $\theta$ is determined by the spacing of the planes given by the formula for $d$ in the introduction.
4. Determine the ball bearing spacing a from your scattering results and compare with directly measured values.