Department of Physics and Astronomy, Stony Brook University
Stony Brook University   |   Introlabs Main Page   |   PHY 133 Webpage

PHY 133 Laboratory
Simple Harmonic Motion
TABLE OF CONTENTS
Introduction
Equipment
Background
Procedure
Analysis
Discussion Topics
References and Tools
Introduction

In this lab, we relate the frequency of an oscillating spring to the spring constant of the spring and the mass on that spring.

We also observe conservation of energy in spring-based systems.Hoveroverthese!

Back to Top
Equipment
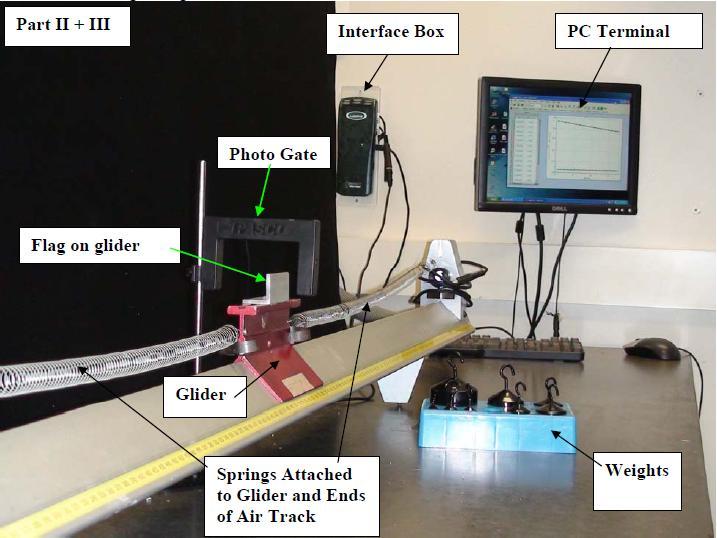
SHM equipment
Back to Top
Background

The period of an object oscillating on the end of a spring is given by the formula:1

$$T=2\pi\sqrt{\frac{M}{k}}\label{T}$$

Here, the spring constant \(k\) comes from the usual definition by Hooke's law, in terms of the force of the spring at some displacement from the equilibrium position \(x\)1:

$$F=-k(x-x_0)$$

If we let \(M\) denote the mass of the object oscillating, this accurately describes an ideal situation in which springs are massless. There is actually a correction2 when we consider the case of springs whose mass is not negligible. If we let \(M_G\) be the mass of the things oscillating (the glider, potentially plus more) and \(M_S\) be the mass of the springs, then the effective mass M (which we plug into the above formula) is defined by:

$$M=M_G+M_S/3$$

We will also make use of the potential energy stored in a spring:

$$U=\frac{1}{2}k(x-x_0)^2$$

Note that the total kinetic energy also uses the same effective mass \(M\) in place of the mass of the glider.

Back to Top
Procedure

Part I: Measuring the Spring Constant

In this part, we will measure the the displacement for various amounts of force, and use the slope to determine the spring constant.

First, disconnect the springs so the cart can move freely,1 and (as always) level your air track.3

While you have everything disconnected, record (at the top of Part II) the mass of your glider and the mass of the two springs (combined)2.

Then, reconnect the two springs, each from one end of the cart to the corresponding end of the track. Then, loop a string (tied to the cart) through the pulley on the other end (ensuring it doesn't get tangled with your spring).

Hang a 20g mass from the spring, and record the position with this mass.3 Take the uncertainty in hanging mass as 0.1g. Then increase the mass to 40g, and repeat (in increments of 20g) up to 100g.4

Part II: Measuring the Oscillation Frequency

Now, remove the string (or wrap it around the cart, so that it's out of the way). We won't need it for the rest of this experiment.

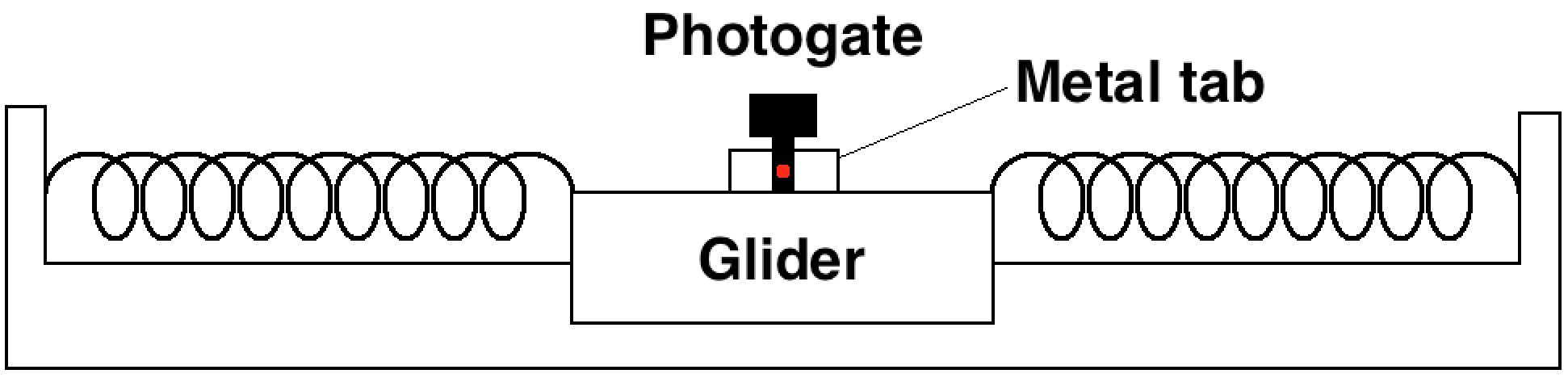
Open "SimpleHarmonic_Period" and set up the photogate, as usual.4 Place the photogate over the rest position of the mass (although the exact position isn't too important).

Begin with the glider alone. Record the additional mass as 0g. Pull the mass back, press "Start Collection," and have the mass oscillate back and forth (with an amplitude big enough to have a few swings back and forth, but small otherwise - don't stretch the springs too much). Then press "Stop Collection."

If the period seems roughly consistent between oscillations, record that period. (Neglect uncertainty in period.) Otherwise, run another trial.

Now: add a 20g mass to the top of the cart, record this as the "Additional Mass," and measure the new period.5 Repeat for three more 20g masses.6

Air Track for Parts II & III
Air Track, springs and glider in Parts II & III

Part III: Observing Conservation of Energy

Take all the masses off your cart. Measure the width of the flag on the cart, and record that on your sheet.

Now, open the LoggerPro file "SimpleHarmonic_Velocity". Double-check that the photogate is still connected and is centered over the middle of the cart's rest position.

Drag the cart some distance (~30cm) from its equilibrium position, and measure this displacement.7 Press "Start Collection," let go, and record the difference in time between when the photogate becomes "blocked" and when it becomes "unblocked" (in order to extract maximum velocity).

Back to Top
Analysis

Part I: Measuring the Spring Constant

For each hanging mass, calculate the tension. Propagate uncertainty.

Make a plot of tension vs. displacement (with appropriate error bars). Record the spring constant you measure from this plot (in the Part II section).

Part II: Measuring the Oscillation Frequency

Calculate the effective mass of the base glider-plus-springs system, and propagate uncertainty. Then, add on the additional mass for each data point to get the total effective mass, and propagate uncertainty.8

Calculate period squared for each period. Then, make a plot of period squared (no error bars) vs. total effective mass.

From the slope, calculate the spring constant (and propagate uncertainties). Compare your results to Part I (answer the question in the data table).

Part III: Observing Conservation of Energy

Calculate \(v_0\) using your flag width and time difference.

Calculate maximal kinetic energy (using the effective mass of your system), and propagate uncertainty. (Note KE is maximal when PE=0, at the center point of oscillation.)

Calculate maximal potential energy (using your measured spring constant from Part I), and propagate uncertainty. (Note PE is maximal when KE=0, at the initial point of release.)

Back to Top
Discussion Topics

Your TA will ask you to discuss some of the following points (they will tell you which ones):

  • Effective Spring Constant: In Part I you measured the keffective of the two springs acting together. If the two springs had k1 and k2 individually, how would they combine to get keff?
  • Effective Mass: In our analysis we use Meffective to more accurately include the mass of the springs. If we neglected this correction (ie. just used mass of the glider and the added weights) what would happen to our experimental value of k? Tell whether the k value from Part II would be larger, smaller or the same and try to make an estimate of how large any change would be.
  • Log-Log Plot: Take your data from Part II, and make a plot of \(\ln(T)\) vs. \(\ln(M_{eff,tot})\). (Ignore what the units on your axes are; that's a somewhat complicated discussion.) What should your slope be? (Hint: take the \(\ln\) of equation \eqref{T}.) Does your actual slope agree? (This is a quantitative way of testing that we have the correct relationship, beyond just seeing that the data looks "pretty linear.")
  • Systemic Error: Leveling Air Track: We level the air track in this lab because it's good lab procedure in general, but in fact in this lab a not-level (but still straight) air track shouldn't change any of our results. Explain why this is true (for each part).2
  • Systemic Error: Air Track Bowing: Let's extend the above assumption, and suppose the air track is bowed, with a height function \(h(x)=ax^2+bx+c\) (with \(a>0\)). In the previous point, we assumed \(a=0\), and analyzed \(b\); now, we'll assume \(b=0\) (for simplicity) and \(c=0\) (since this doesn't matter), and analyze the effect of \(a\). Calculate the net gravitational+normal force on this system, and consider what the impact is on our experiment.3
    • There is a way account for this additional force by redefining our spring constant as a new, total "effective" spring constant (in the sense that all our formulas still work, just with a different \(k\)). Identify the new "effective" spring constant in terms of the old spring constant and \(a\), and explain why this works.
    • A reasonable "very large" value for \(a\) is \(0.01m^{-1}\); given your numbers, how does this bending "correction" (which we deliberately overestimated, to give an upper bound on thi systemic error) compare to your original spring constant?
Back to Top
References and Tools

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

PHY133/134 Plotting Tool

Photogate Reference Document

Air Track Reference Document

Hovering over these bubbles will make a footnote pop up. Gray footnotes are citations and links to outside references.

Blue footnotes are discussions of general physics material that would break up the flow of explanation to include directly. These can be important subtleties, advanced material, historical asides, hints for questions, etc.

Yellow footnotes are details about experimental procedure or analysis. These can be reminders about how to use equipment, explanations of how to get good results, or clarifications on details of frequent confusion.

For a review of simple harmonic motion, see Katz, Chapter 16 or Giancoli, Chapter 14.

For more detail on where the factor of 1/3 comes from, see here.

See Air Track Setup Instructions.

See the Photogate Setup Instructions.

Check that it does, in fact, glide freely when released, and that there's not a significant amount of friction.

Use Table with Glider Masses and 9.7±0.1 grams each for the springs.

Ideally, you want to measure this precisely, so you want a good fixed point to measure from. Therefore, for this, the end of the cart makes more sense as a reference point than the middle of the cart (since the end of the cart is an easy identifier that's right above the ruler on the air track).

Depending on the orientation of your air track, it may make sense to record all your positions as negative - do this if you wish. (If the positions are decreasing as you hang more mass, making them all negative will give you a positive slope.)

There are various ways to do this, but the simplest is to hang it off the side (rather than put it on top, etc.). Just make sure it doesn't block your photogate.

In the interest of not having friction (as the masses exert torque on the cart, making it drag on the air track), make sure you balance out the locations of the masses as much as possible (i.e., don't put them all on the same side).

As with your position measurements earlier, it is best to measure the displacement using a position you can measure accurately, like one of the endpoints of the cart.

We neglect uncertainty in additional mass, so this uncertainty "propagation" is very easy.

Note that \(x\) is the position of an object and the equilibrium position is \(x_0\). So, the displacement from equilibrium is given by \(x - x_0\).

Hint: there are two ways to show this mathematically, taking into account the "extra" effects of gravity. One is to show that the force still takes the term \(F=k(x-x_0)\) for some \(k\) and \(x_0\) (and for each, you should either show that they don't change or explain why they don't matter). The second is to do the equivalent result for potential energy - show that \(U=\frac{1}{2}k(x-x_0)^2\) still (again, potentially-different \(k\) and \(x_0\), explain why differences that occur don't matter).

We are neglecting the effect that the curvature has on our length measurements. I.e., if the spring is straight but the cart moves along a track, the two distances won't be exactly equal, etc.... But we can ignore this (as a "leading-order approximation") if \(a\) is reasonably small, because these impacts will be proportional to \(a^2\) (if not a higher power of \(a\)).