
Properties of Fluids, Fall 2025

In this lab, we will study the behavior of fluids in both static and dynamic cases.Hoveroverthese!
Since this is a partially simulated lab, you will find some values are already in your data sheet. Put your student ID number (or another unique 9-digit string) in the green box to get your personalized data.
In studying introductory physics, we typically start by treating objects as single points, which can translate in one or more dimensions. Next, we allow objects to have an extent which can rotate (as well as translate). Up to that point, all materials we consider are solids, which do not change shape when moving.
To prepare for the next level of complexity, we need the definition of pressure: \(P\) is the Force per unit Area exerted on one part or the whole of an object \( P= F/A \). Most textbooks then consider the deformation (compression, extension, shear) of solids and the pressure required to cause the material to exceed its elastic limit and fail.
Liquids and gases are examples of fluids1, which flow under a pressure or, if confined, transmit that pressure throughout the fluid volume. In this experiment we will investigate a liquid (water) which we will treat as an incompressible fluid (also non-viscous, until Part III).
In the motion of an incompressible, non-viscous fluid, we have conservation of energy. Combining this with the conservation of matter (ie. the fluid does not evaporate or react chemically) we arrive at the Bernoulli equation and Continuity condition relating conditions at points 1 and 2 in the system. \(P\) is the measured pressure, \(\rho\) is the density1, \(v\) the fluid velocity and \(A\) the area of the flow (ie. pipe inner area).
$$P_1 + \frac{1}{2} \rho v_1^2 + \rho gy_1 = P_2 + \frac{1}{2}\rho v_2^2 + \rho gy_2 $$ $$A_1 \rho_1 v_1 = A_2 \rho_2 v_{2} $$In Part I we will deal with a special case: hydrostatics. In this situation the velocity terms in Bernoulli's Equation are zero. The hydrostatic term, \(\rho gh\) and Pascal's Principle (any outside pressures act throughout the fluid) combine to give Archimede's principle: if \(V_{displaced}\) is the volume of fluid displaced by an object then the buoyant force is given by
$$ F_{buoyant} = \rho_{displacedfluid} \, g V_{object} $$Part II makes use of a PhET simulation of an ideal fluid in a pipe. We will examine a dynamic case but with no change in (average) height, so the hydrostatic terms \(\rho g(y_1 - y_2) =0\), leaving the Bernoulli equation as:
$$P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2}\rho v_2^2 $$In Part III we look at a deviation from Bernoulli for non-ideal fluids which exhibit viscosity but do not undergo turbulence. A simple model for viscous fluids is to assume laminar flow; this works for a regime of flow where the Reynold's Number is low. Internal friction in the fluid leads to energy loss, which can be seen as a pressure difference across a small pipe (or capillary) which depends on the flow rate. The Hagen-Poiseuille's Law state that \(R\), the resistance to flow for a pipe, depends on length \(L\), area (therefore radius \(r\)), the volume flow rate \(\frac{dV}{dt}\) and the dynamic viscosity of the fluid \(\eta \)2 in the following way:2:
$$ \Delta P = R \frac{dV}{dt} \ \ and \ \ R = \frac{8 \eta L}{\pi r^4} $$This flow regime, where pressure and flow rate are proportion, is very common in physical systems. In particular, the arteries and capillaries in the body are small enough that the flow obey this (non-ideal) rule.
Part I: Archimede's Principle
Open the PHeT simulation Buoyancy: Basics and choose "Explore".
- By default you will be given a \(2.00\) kg wood block floating in \(100\) Liters of water.
- Take the wooden block out of the water and place it on the dry scale. You will see a mass of \(2.00\) kg gives a weight (Force of gravity) of \(19.6\) Newtons.
- Use the sliders in the upper right to choose a custom density less than \( 1.0\) kg/L and any volume you like. Record the mass of Block A and weight.
- Place the block back in the water. Record the volume indicated on the left of the tank.
- Now place the block above the submerged scale and change the height of the scale until it has a non-zero reading. Record the volume indicated on the left of the tank and the force indicated on the submerged scale. Hit the green \( + \) sign on "% Submerged" and record the value.
- Now, use the sliders in the upper right to choose a custom density greater than \( 1.0\) kg/L and any new volume you like. Lower the submerged scale to the bottom of the tank. Record the tank liquid level, mass, density and volume of the block, plus the force indicated on the submerged scale.
- Last, play wth all of the buttons and sliders and checkboxes. Take a screen shot which proves that you have interacted with the simulation .
Part II: Pressure and Flow Velocity
Go to the PhET simulation Pressure and Flow. This is a legacy simulation; the CheerpJ Browser-Compatible version is the better choice. Select the tab for "Flow".
- Set the fluid density and flow rates close to the target values from your data sheet. Record the actual values.
- Use the tools to get measurements of flow velocity, pressure and pipe area for two locations on the pipe with \(v_2 \approx 4v_1\).
Details on a method to do Part II
- Fluid density can be set with a drag bar in the lower right of your screen. Flow rate can be set with a drag bar in the upper left.
- Drag down two speed gauges and set them into the flow at about the first handle and the fourth handle. Are the flow velocities about the same? Use the handles to make the speed at the 4th handle ~ 4x the speed at the first handle. The handles can make the pipe larger or more narrow. Record the speeds (velocity \(v\)).
- Drag down two pressure gauges and measure the pressure \(P\)at the same locations. You may need to move the speed gauges out of the way to put the pressure gauges where you like. Notice how the \(P\) changes with small movements and consider that when you assign experimental uncertainty.
- Turn on the Flux Meter with the check box in the menu on the upper right of your screen. Drag the Flux meter to each of your two locations to find the Area \(A\) of the pipe. Alternately, you may also choose to grab the Ruler tool and measure the pipe diameter at each location.
- Take a screen shot at some point in your investigation, showing the pipe and some gauge readings. Include this screen shot in your lab report.
Part III: Poiseuille's Law
In this experiment, a fluid is forced to flow through a small capillary by hydrostatic pressure. The capillary is chosen so that water will exhibit nearly laminar flow and obey the Hagen-Poiseuille law. As the experiment progresses, the change in column height (and, therefore \(\Delta P\)) is related to volume flow \(\frac{dV}{dt}\) by that law.
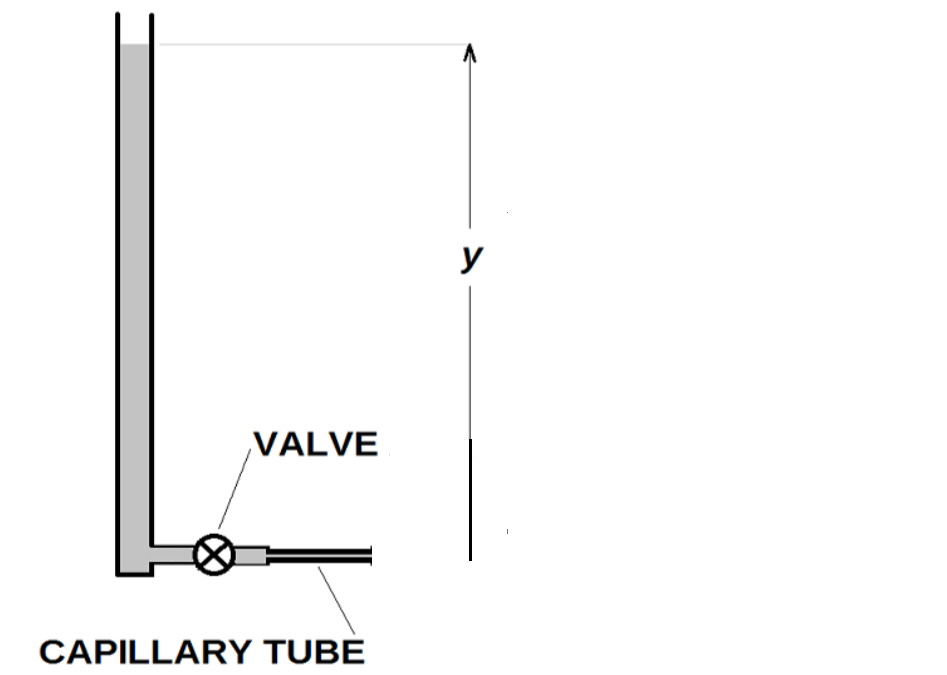

- The apparatus is a vertical tube (column) which is open at the top and connected to a valve and capillary tube at the bottom.
- The flow valve is closed, so that we can fill the vertical tube.
- Next we carefully pour water into the column until \(y_0 \approx 50\)cm. Your particular value is given in your data. Note that \(y_0 \) is measured from the (vertical) center of the capillary tube.
- We will simultaneously start a timer and open the valve; the water level in the column will start dropping and water will pour out of the capillary. Data for \(y(t)\) and the elapsed time \(t\) at 30 second intervals is given in the data sheet.
- Note that a lab room temperature in Celsius is given in your data sheet.
More information about non-ideal fluids, considering viscosity
Presented here is the derivation of Equation 8, which we will use to find the resistance to flow of a small tube (capillary).
- The height of the column of water is called \(y \).
- \(V_{cylinder} = \pi r^2 (height) = A_{cyl}h\). So, flow into cylinder i would be \(\frac{dV}{dt} = \frac{d}{dt}(Ah) = A\frac{dy}{dt}\). Positive flow through the capillary out into the air decreases \(y\), so, replacing with y, \(\frac{dV}{dt} = -(A)\frac{dy}{dt}\)
- We look at the entrance and exit of the capillary. There are the Bernoulli terms plus a \(\Delta P\) from the resistance to flow. Both columns are open to air (\(P_{1, external} = P_{2, external}\)) and the velocities \(v_1 = v_2,\) (this must be true by continuity), so \( \Delta P = \rho g y = R \frac{dV}{dt}\).
- Thus, \(R \frac{dV}{dt} = R (-A)\frac{dV}{dt} = \rho g y\). We separate variables to get: $$ \frac{dy}{y} = -\frac{\rho g}{RA}dt $$
- Then we integrate both sides: $$ \int_{y_0}^y \frac{dy}{y} = \int_{t=0}^t -\frac{\rho g}{RA} \, \mathrm{d}t $$
- Resulting in $$ ln(y/y_0) = -\frac{\rho g}{RA}t $$
- We will plot \( \ln y\) versus \(t\) so our final form will be $$ ln(y) = -\frac{\rho g}{RA}t + ln(y_0) $$
Part I: Archimede's Principle
State the equations which are acting in these processes and show the relationships between values. In particular, derive the reading on the submerged scale in each case.
Since the "data" are from simulation, there is no relevant error analysis to do.
Part II: Pressure and Flow Velocity
Use your values for \(P_1\),\(v_1\),\(P_2\),\(v_2\) and the density of fluid, \(\rho\), to test if Bernoulli's Equation (Eq 1) is satisfied (ie used) by this simulation.
Use your values for \(A_1\),\(v_1\),\(A_2\), and \(v_2\) to test if Continuity of mass flow (Eq 2, with \(\rho\) constant becomes \(A_1 v_1 = A_2 v_{2}\) ) is satisfied (ie used) by this simulation.
Part III: Poiseuille's Law
Calculate \( \ln (y) \) and assign the same relative uncertainty as for \(y\)
Make a plot of \( \ln (y) \) vs. elapsed time \(t\). The slope should be \( Slope = -2ρg/RA\).
Use your slope (and knowledge of room temperature) to extract a value for \(R\), the flow resistance. Compare to the theoretical value obtained using Equation 5 with room temperature \(T\) (in \(^\circ\)C), radius of the capillary \(r_{capillary} = 0.5 \)mm, and the viscosity of water \(\eta = 1.002 + .024(20- T) x 10^{-3}\)Pa-sec. You will need to look up the density of water, \( \rho \), at your temperature.
Your TA will ask you to discuss some of the following points (they will tell you which ones):
- Floating Objects: Make a Free Body Diagram on the submerged block and show the force equations. Use Archimede's Principle (Equation 3).
- Systemic Error: Uniformity of Temperature: We did not specify any temperature controls or measurements in Part I. Estimate how large would the effect be if the tap water used for Part 1 was ~55\(^\circ\)F.
- Height of the pipe ends in Part II A feature of the simulation we did not use is that the pipe ends may be raised and lowered. If we made the pipe ends at different heights, how would our results for testing the Bernoulli Equation and Continuity expression be affected?
- Use of Logarithms in Part III Properly, we should have taken the natural logarithm of a ratio, such as \( y/y_0 \). Why? Where does the \( \ln (y_0) \) appear in the plot of \( \ln (y) \) vs. elapsed time \(t\) ?
- Temperature correction in Part III Is our inclusion of a temperature dependence of viscosity \(\eta\) necessary in this experiment? make a quantitative argument why or why not.
- Other hydrostatic terms in Part III We did not specify or measure the vertical distance above the ground for the apparatus. Comment, quantitatively would be preferred, on whether this is justified.
Hovering over these bubbles will make a footnote pop up. Gray footnotes are citations and links to outside references.
Blue footnotes are discussions of general physics material that would break up the flow of explanation to include directly. These can be important subtleties, advanced material, historical asides, hints for questions, etc.
Yellow footnotes are details about experimental procedure or analysis. These can be reminders about how to use equipment, explanations of how to get good results, or clarifications on details of frequent confusion.
For a review of ideal fluids, see Giancoli Chapter 13 or Katz Chapter 15.
For more on non-ideal fluids, see Giancoli Chapter 13, Sections 11-12 or Katz Chapter 15, Section 6.An excellent alternative resource is HyperPhysics on Laminar Flow and other links therein.
In general, the density \(\rho \) can be different at points 1 and 2 but will be the same for our experiment.
The form of this relation might remind one of Ohm's Law for flow of electrical current through a resistance, driven by a voltage:\(V = IR \) where \(R = \rho L/A \). An important difference is that this model for fluid flow assumes laminar flow, which has maximum velocity in the center of the pipe and \(v=0\) at the pipe wall. This leads to the \( 1/A^2\) or \(1/r^4 \) dependence for viscous fluid flow, rather than the \( 1/A\) in electrical resistance.
\(m\prime \) is often called the "apparent mass" or, colloquially, the "weight under water".
When this apparatus is used for a full lab we often investigate the effect of putting multiple capillaries together in series or parallel.
Another variation is to have two cylinders, one nearly full of water and one nearly empty, with the valvle and capillary tube between them. In this case the relevant \( \Delta P\) is created by the water column height difference.