In this lab, we will observe Newton's second law using an Atwood machine.^{Hoveroverthese!}

• 1 Pulley w/ String and Stand
• Various Masses
• 1 Photogate setup
  • Photogate
  • Interface box ("LabPro")
  • Computer
• Record data in this Google Sheets data table

An Atwood machine consists of two masses attached to a string draped over a pulley.¹ Ideally, both the string and pulley are massless and the pulley is frictionless.

Adding the forces on each mass gives us the following picture:

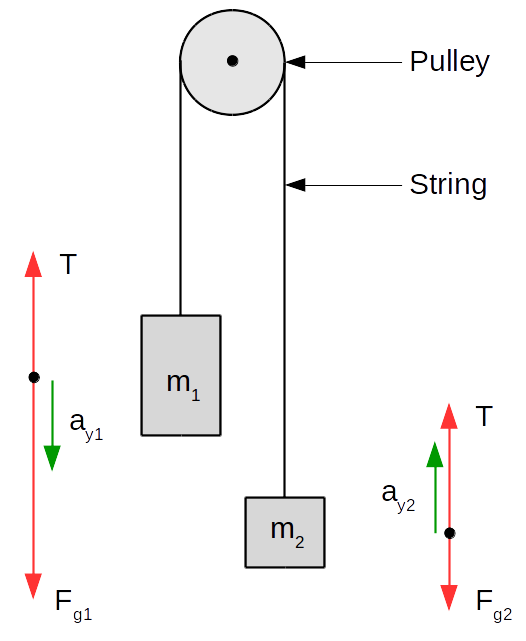
We can then solve for (the magnitude of) \(T\)¹ and \(a_y\) (operating under an assumption that \(m_1>m_2\)):

$$a_y=\frac{m_1-m_2}{m_1+m_2}g\label{accel}$$ $$T=\frac{2m_1m_2}{m_1+m_2}g\label{tension}$$

Begin by opening the "Atwoods" file. Ensure that your pulley is set up with the photogate plugged in. Make sure that when you spin the pulley, the photogate switches between the "blocked" and "unblocked" states.

Click on "Data->User Parameters" and ensure that the photogate distance is entered as .0154m.¹ This is 1/10 the circumference (measured at the radius where the string sits), which is the "distance per spoke" (since the pulley has 10 spokes). The photogate is blocked/unblocked by the spokes, thus this is the distance the masses travel each time the photogate goes through a blocked-unblocked cycle.

If there is not already a string with a loop in each end, make one. Make your range of motion as large as possible: make the length so that when one mass is almost on the floor, the other mass is almost at the pulley. You want at least a half-meter range of motion, and more is better.²

Over the course of this experiment, we will use the following mass combinations:³

• 30g and 50g
• 40g and 60g
• 50g and 70g
• 60g and 80g
• 80g and 100g

Connect the first mass combination.⁴ Hold the string of the light mass in a position where the light mass is low and the heavier mass is high. Keep the string as vertical as possible, to avoid the string falling off the photogate or the masses colliding.⁵

Press the green button, wait a second, then release. Catch the small mass before it hits the pulley. (If the string falls off the photogate before the end of your trial, retake your data.)

Stop recording. Highlight the region where the data on the velocity vs. time graph looks linear (ignore the beginning and ending parts), and add a linear fit.⁶ If the masses collide, you should only take before that collision; if there is not enough data before the collision to run a good fit, redo the trial.

Record the slope of this fit as the acceleration of the mass for this trial. Then, remove this fit (press the "x") for the next trial.

Perform two more trials with this mass combination.

Finally, repeat (do three trials) for each mass combination.

For each mass combination, compute the average acceleration and the uncertainty in average acceleration using the usual formulas.

Calculate the quantity \(\frac{m_1-m_2}{m_1+m_2}\).⁷ This will not have uncertainty, since we have neglected uncertainty in the masses.

Make a plot of average acceleration vs. \(\frac{m_1-m_2}{m_1+m_2}\) (with appropriate error bars).

Interpret the slope of your graph, and extract from it a measurement of \(g\). Answer the question on the data sheet about whether your result agrees with expectation.

Your TA will ask you to discuss some of the following points (they will tell you which ones):

• Theoretical Relationship:
  • Derivation of Acceleration and Tension: Beginning with the force diagrams, show that equations \eqref{accel} and \eqref{tension} both hold.
  • Reduction to Dimensionless Parameters: We know we can express both \(a\) and \(T\) as a function of \(m_1\), \(m_2\), and \(g\). Using dimensional analysis,², we know the dependence on everything except dimensionless combinations of those variables. Take \(\lambda=\frac{m_2}{m_1}\) (there are no other independent dimensionless combinations), and, starting with equations \eqref{accel} and \eqref{tension}, show that the following relationships hold: $$a_y=\frac{1-\lambda}{1+\lambda}g\label{aydless}$$ $$T=\frac{2}{1+\lambda}m_2g\label{Tdless}$$
  • Limiting Cases: What would the acceleration and tension be if the two masses were equal? What if \(m_1\) was much bigger than \(m_2\)?² In the latter case, you should find a better approximation than "the tension is zero."³
• Systemic Errors:
  • Pulley physics: What would the impact be (qualitatively speaking) on our measurement of \(g\) if the pulley had a non-negligible mass or friction?⁴
  • Release physics: What would the impact on our measurement of acceleration be if we gave the string a small jerk initially? (Remember that we only looked at the straight-line part of the graph for our fit.)
  • String mass: Firstly, just approximating the string as "more total mass" (with no relevant gravitational force), what would be the impact on our measurement of \(g\) of a massive string? Now that you've thought through that, let's also suppose that the string's weight is important: what would be the impact on the shape of our \(v\) vs. \(t\) plot?
  • Wobbly wheel: If you spin the pulley slowly with nothing on it, you will often find that it comes to some preferred resting position (so that, when it's near this position, it behaves almost like a pendulum - it spins, stops, and spins back, until one particular spoke comes to rest at the bottom). What physical explanation can you give for this effect? What impact would this have on a freely-spinning wheel? Assuming our acceleration measurement is taken from many spins of the wheel, would this have a systemic impact on our acceleration measurement?
  • String width: Suppose we used a particularly thick (but still massless) string. What impact would this have on our measurements? (Hint: think about what \(D\) represents, and how a thick string could throw this off.)
• Uncertainty in Masses:
  • In General: Suppose that \(m_1\) and \(m_2\) had uncertainties. Then, we would need to perform a propagation through \(\frac{m_1-m_2}{m_1+m_2}\). This is nontrivial, due to the reasons discussed in Section A.3.3 of the Error Analysis Guide - you can't just break it up into elementary calculations. Let's do this propagation properly (only using single-variable calculus) by doing the following steps:
    • Express \(\frac{m_1-m_2}{m_1+m_2}\) purely in terms of \(\lambda=\frac{m_2}{m_1}\). (Assume \(\lambda<1\), since that is the case in this setup.)
    • Determine the uncertainty in \(\lambda\) in terms of the uncertainty in the masses (which is as straightforward as it looks).
    • Using the discussion in Section A.3.1 of the Error Analysis Guide (in particular, the general one-variable error formula provided in that section), determine the uncertainty in the expression you found in the first step, in terms of the uncertainty in \(\lambda\).
  • Application to Our Numbers: Take your formula from the previous discussion point. Work through these calculations with the first data point (\(m_1=30\)g, \(m_2=50\)g) using an uncertainty in each mass of \(0.1\)g (which is reasonable³). Compute the relative error in \(\frac{m_1-m_2}{m_1+m_2}\), and compare this relative error to your relative error in \(a_y\). How much does this uncertainty matter?
• Alternative Description of Atwood: Here's a different way of looking at the Atwood machine. Since the (massless, frictionless) pulley doesn't do anything itself, we can imagine rotating the smaller mass system by 180 degrees and stacking it on top of the other system (with gravity now pulling "up" on the smaller mass). Tension is now an internal force that we ignore, and this leads to a very easy derivation of \eqref{accel} and \eqref{tension}. Explain this derivation.

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

PHY133/134 Plotting Tool