In this lab, we will investigate the basic principles of ray optics, emphasizing Snell's law and the Law of Reflection.^{Hoveroverthese!}

• Optics Kit:
  • Laser Apparatus
  • Triangular Prism
  • Plane Mirror, 2D Curved Mirror
  • 2D Converging & Diverging Lenses
  • Graph Paper
  • Laminated Protractor Paper
  • Mini-ruler
• Record data in this Google Sheets data table

Basic Principles of Reflection and Refraction

There are two phenomena that occur when a light beam hits an interface between two different kinds of material: refraction and reflection.¹

Refraction occurs when the light is transmitted into the new material, but at a different angle than it came in. Reflection occurs when the light reflects back into the material whence it came.

In both cases, we first draw a line perpendicular to the interface, which we call the normal. The basic angles we deal with in optics are the angles between a beam of light and the normal, as seen below:

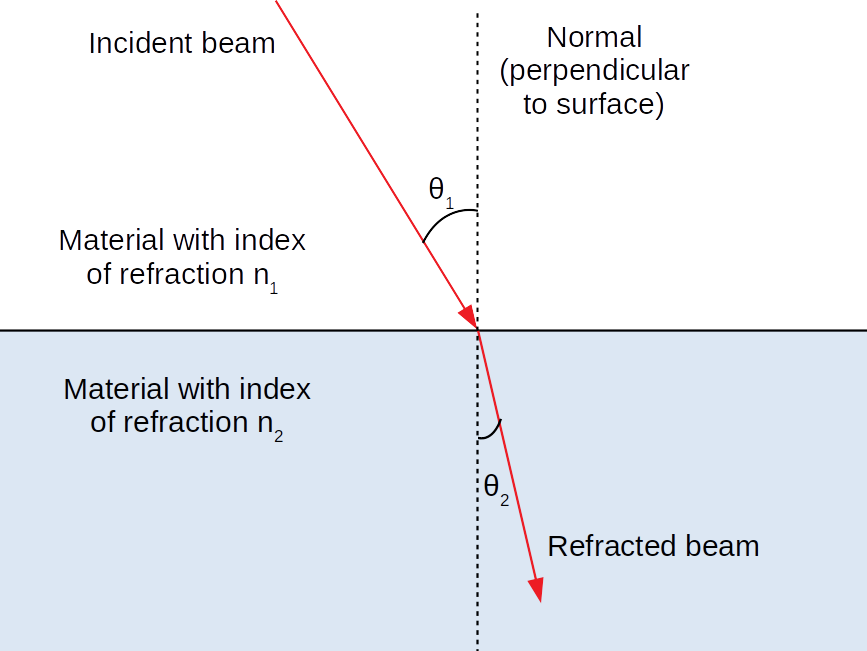
For reflections, the law of reflection states that the incoming angle (with respect to the normal) and the outgoing angle (w.r.t. normal) are the same. This is true regardless of the details of the reflection (whether you are going "inside" a material to "outside," vice-versa, or bouncing off a mirror).

For refractions, the angles are instead governed by Snell's law:

$$n_1\sin(\theta_1)=n_2\sin(\theta_2)\label{snell}$$

Here, we label the two sides of the interface by \(1\) and \(2\) (with, usually, \(1\) being the side of the incoming beam, and \(2\) being the side of the refracted beam). The quantities \(\theta_1\) and \(\theta_2\) are then the angles (w.r.t. normal) of the light beam on the respective sides of the interface.

The quantities \(n_1\) and \(n_2\) are the indices of refraction of the materials on each side of the interface. The index of refraction is a property of a material which describes how fast light moves in a material (\(v\)) vs. in vacuum (\(c\)):

$$n=\frac{c}{v}$$

Hence, \(n=1\) for vacuum, and approximately so for air. Otherwise (generally), \(n>1\).¹

Total Internal Reflection

When a beam of light moves from an area of higher \(n\) to lower \(n\), depending on \(\theta_1\), it is possible that there is no \(\theta_2\) that will cause Snell's law to hold.

In this case, no light can be refracted, and we have what is called total internal reflection: all light is reflected back into the material (at an angle given by the Law of Reflection).

This phenomenon happens if the incident angle (w.r.t. the normal) exceeds some critical angle \(\theta_c\). If the index of refraction in the region of the incident beam is \(n_1\) and on the other side of the material boundary is \(n_2\), then \(\theta_c\) is determined by setting \(\sin(\theta_2)\) equal to \(1\) in equation \eqref{snell}, producing the formula:

$$\sin(\theta_c)=\frac{n_2}{n_1}$$

Understanding Intensities

You may wonder how much light is reflected and how much light is refracted, as a function of angle. Unfortunately, this is a surprisingly complicated question, and a full formula for the intensity of the reflected vs. refracted beams are beyond the scope of this course. Nevertheless, one basic principle that governs these powers can be understood.

The intensity of the beam is the power (energy per unit time) transmitted per unit area. Therefore, by conservation of energy, if no light is absorbed (which is a separate possible phenomena), the total incoming intensity has to equal the total outgoing intensity (added over all outgoing beams).²

Mirror Basics

Thus far, we have focused on reflection and refraction by flat surfaces. While the principles are the same for curved surfaces (just with a "normal" that varies over the surface of the material), the computations get more complicated to do "exactly."

That said, most of the real use of optics comes from using curved surfaces to focus or defocus light, so it's important to work with. Here, we simplify by working primarily with arrangements of one particular kind of curved surface, a spherical mirror.²

There are two kinds of curved mirrors: concave, which which bend "inwards" (toward the source of light) and convex, which bulge "outwards". Formally, a concave mirror has its center-of-curvature on the side of the incoming light (\(R \gt 0 \)) and a convex mirror has its center-of-curvature where the light cannot reach (\(R \lt 0 \)).

Suppose a bunch of parallel light beams hit the mirror. A concave mirror has the outgoing light beams (reflected) focus to a single point, known as the focal point. A convex mirror lens has the light beams bend apart, but in such a way that it appears they all come from a single point behind the mirror.

The forward-displacement to the focal point is known as the focal length, \(f\). (This means that if the focal point is behind the mirror, as occurs for a convex mirror, then the focal length is negative.) A spherical mirror has a focal length which is half of the radius of curvature, ie \(R = 2f \).

An ideal mirror (which makes this focal point exactly) is actually shaped like a (slice of a) parabola. However, it is far easier to manufacture is the spherical mirror. Deviations from the "ideal" focal point due to the mirror being spherical is known as spherical aberration.

Forming Images With Mirrors

A mirror can form an image of something (a visual copy in another place, potentially with another size).

Schematically: consider the light beams that are emitted by some point on our object. The beams that reflect off the mirror will intersect (or appear to intersect) somewhere, which is where a focused image will form.

This intersection may not be "physical" - it may be behind the mirror (i.e., the beams all seem to be coming from a common intersection point). If the beams actually intersect, the image is real; if they do not, the image is virtual.

Typically, we assume that we are using paraxial rays. This allows us to approximate the light's trajectory by assuming that some angles are small and so we can apply the small angle approximation .

Under this assumption, we find the Mirror Equation:

$$\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}$$

Here, \(d_o\) is the distance to the object, \(d_i\) is the distance to the resulting image, and \(f\) is the focal length of the mirror (as defined above).

The sign conventions on these quantities can become complicated when you have multiple lenses oro mirrors, but for the purposes of this lab:

• \(d_o\) is positive (this is true for any "real" object, although may not be for multi-lens systems).
• \(d_i\) is positive if you have a real image, and negative if you have a virtual image.
• \(f\) is positive for concave mirrors and negative for convex mirrors

With these definitions and the small angle approximation , the Mirror Equation is the same as the Lens Equation, but we will not be making use of that fact in this lab.

Part -1: Basic Reflection

Take the giant laminated protractor paper from the kit. In this part, we will measure angles directly.

Put the flat mirror from your kit along the 90-270 line on the protractor (such that the normal is along the 0-degree axis).

Put the laser off at some angle (less than 90 degrees from zero), and point it towards the center of the protractor. Measure both the angles with respect to the normal of both the incoming and reflected outgoing beam using the protractor. Estimate uncertainties.

Part 0: Focal Length of a Curved Mirror

Put the curved mirror and the laser on a sheet of graph paper. Direct the single laser beam along a line and then orient the mirror so that the laser beam reflects back on itself.

Now switch the laser to 3 beams. Record the distance between the mirror and the point where all 3 beams cross, with unceratinty. This is the focal length \( f \).

Switch the laser to 5 beams. Do all 5 beams cross at the same point? Answer questions in the data sheet.

Determine the radius of curvature of the curved mirror, with uncertainty.

Click here for suggestions on determining R.

Part I: Basic Refraction

In this part, we are going to measure all of our angles by measuring distances. This will enable us to measure them with a reasonable degree of precision.

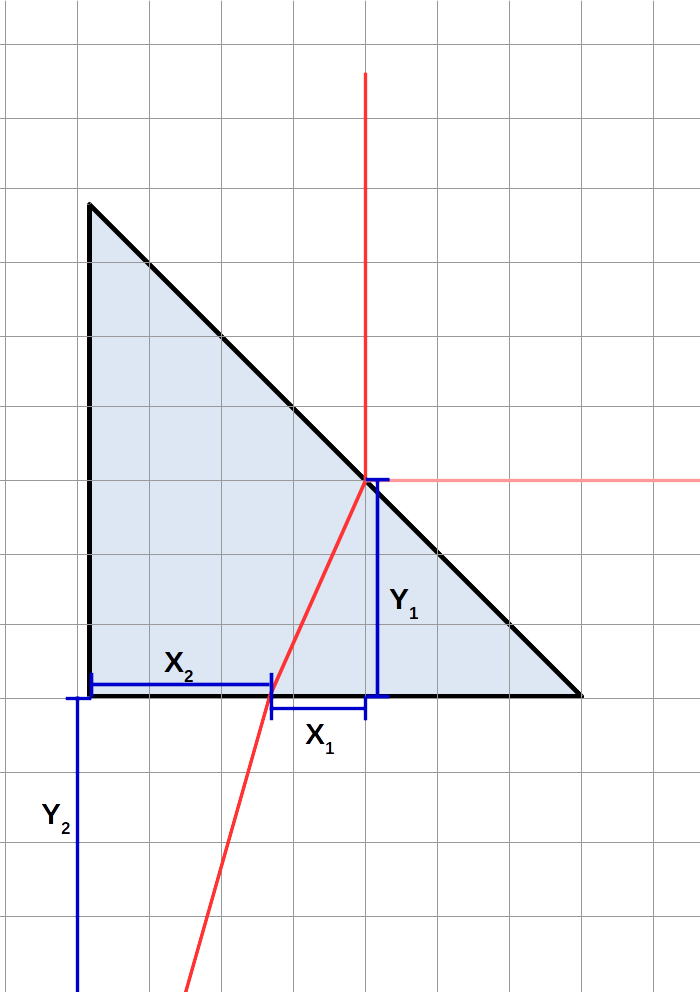
The angles and distances we will look at¹ are shown in the following diagrams. Red lines are the laser beams; in the left diagram, blue lines are normals. (Note \(Y_2\) extends downwards to the location of the light beam at that x-coordinate.)

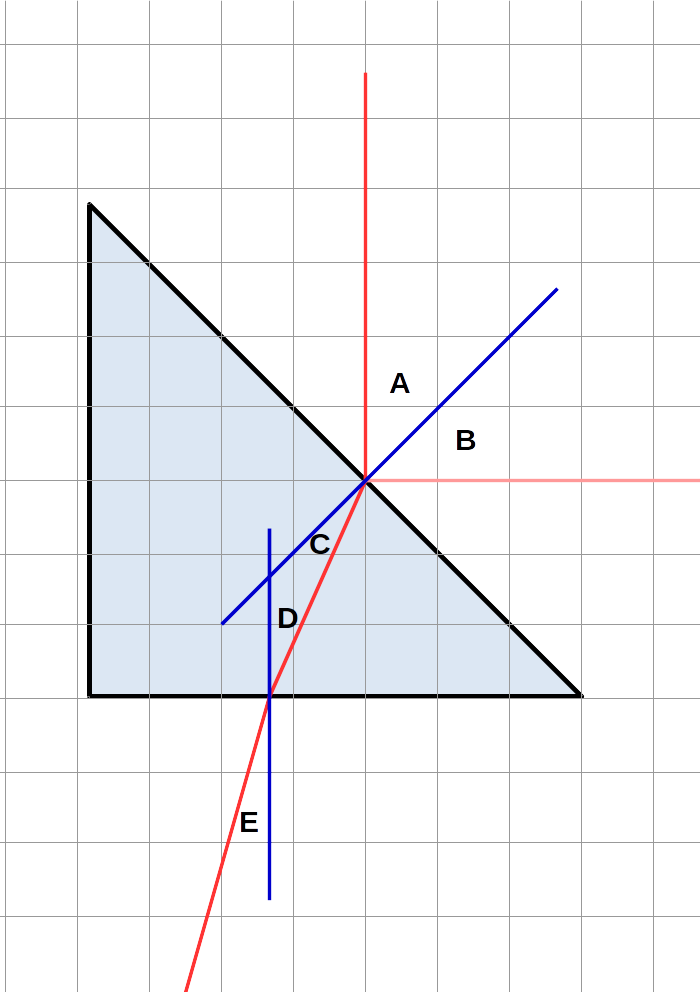
Take the \(45^\circ\) triangular prism, your laser, and one sheet of graph paper. Plug in your laser, and set it to output one beam (middle setting on the switch). Press the button and make sure it shines a beam.²

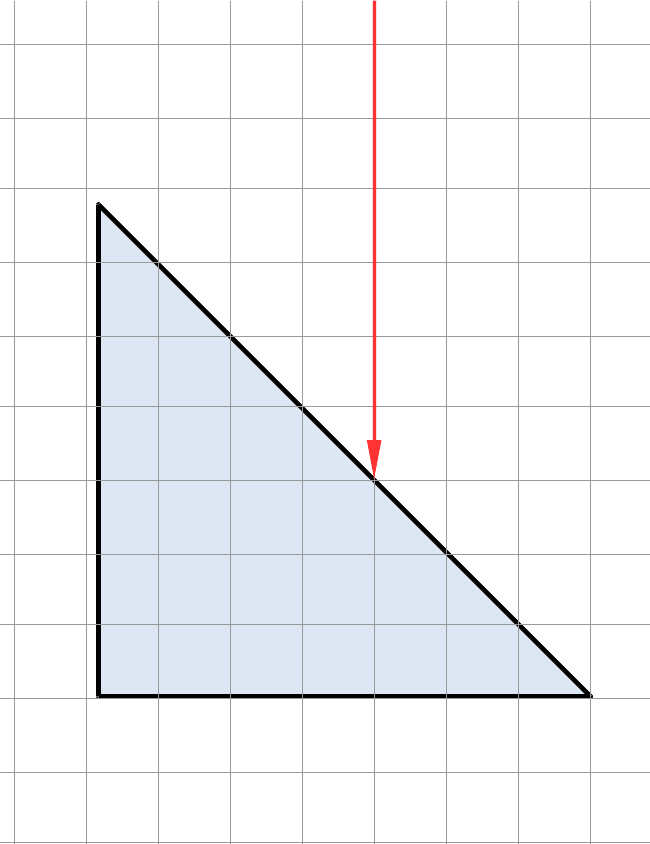
Place the triangular prism on the graph paper such that one of the shorter edges aligns with one of the grid lines. Slide sideways until the \(45^\circ\)-angle-corner of that side is on a grid line intersection. (See diagram below if these instructions are confusing.)

Now, take the laser and shine it on the prism perpendicularly to the edge you lined up, from the hypotenuse side. Line the laser up so that its beam travels along the gridline which has three boxes inside the prism.

Schematically, your setup should be illustrated by the following figure (the location of the left edge of the prism may vary):

Now, measure the distances \(X_1\), \(Y_1\), \(X_2\), and \(Y_2\). Measure as precisely as you can here, ideally to sub-millimeter precision - you'll get better results that way. Estimate uncertainties.

Part II: External Reflection

Set aside the graph paper, and take the giant laminated protractor paper from the kit. In this part, we will measure angles directly.

Begin by lining up the hypotenuse of the trianglular prism with the 90-270 line on the protractor (such that the normal is along the 0-degree axis).

Put the laser off at some angle (less than 90 degrees from zero), and point it towards the center of the protractor. Measure both the angles with respect to the normal of both the incoming and reflected outgoing beam using the protractor. Estimate uncertainties.

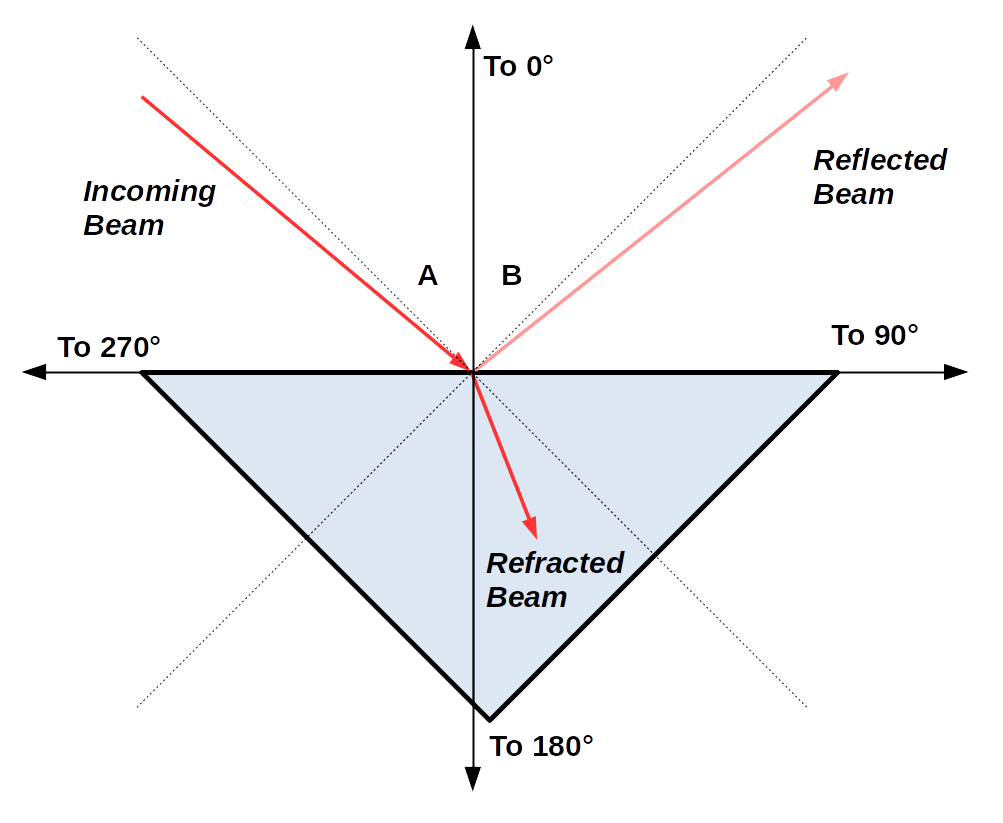
Also take note of the relative intensity of the reflected beam compared to the incident beam.

Replace the prism with the mirror (yes, again).

Take note of the reflected intensity (compared to the incident intensity) for this component. (Think: why a difference?)

Part III: Total Internal Reflection

In this part, we will again measure angles; however, they will be determined with significantly less precision than the last part.³

Place your triangular prism on the mini-protractor so that the hypotenuse is on the +90° line, so the right angle points towards 0°. Shine the laser on the prism in the following way:

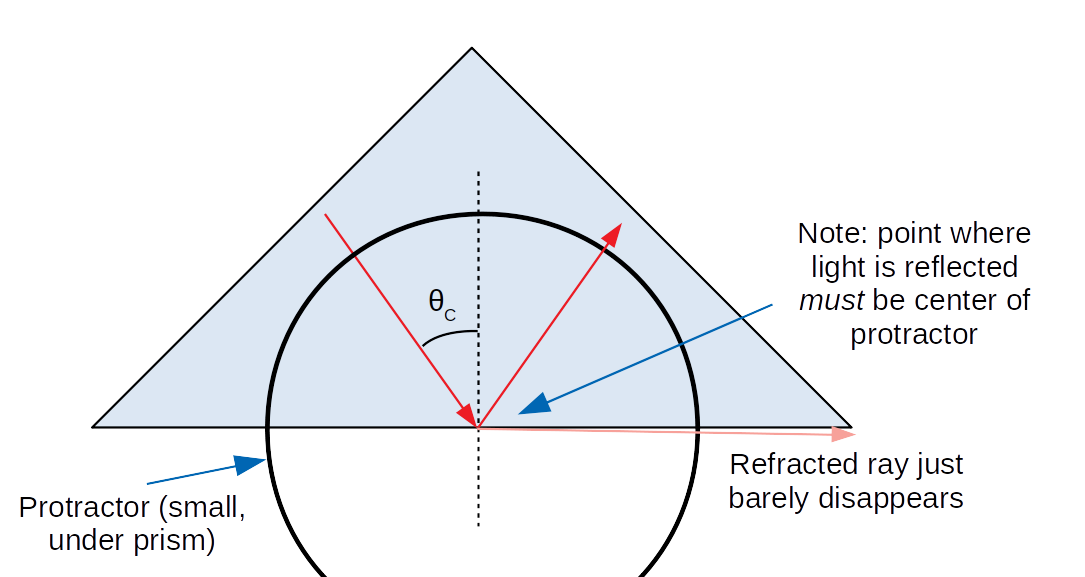
Rotate the laser until you reach the point where the outgoing refracted beam just disappears (by "folding into" the hypotenuse of the triangle). The angle on your protractor (if the laser is still pointed at the center of it!) is now the critical angle.

Adjust your positions until you feel you've got the best measurement of critical angle you can get, and record that value. Estimate its uncertainty (however precise you think you were able to get).

Now, let's make some qualitative observations of intensity. Rotate your prism so it's just outside the angle at which total internal reflection happens (so that you have a refracted beam that is almost gone).

Now, wiggle it slightly. How do the incident, internally reflected, and refracted beams vary in intensity, if at all, as you approach the critical angle (from the direction where the refracted beam appears)? (This is most visible when you're really close to the critical angle.)

Part IV: Parallel Rays Into Lenses

Flick the lever on the laser box so that you get five light beams, and pull out both the converging and diverging lenses.

Begin with the converging lens (the one that looks like a football). Shine the laser through it, and observe what you see. Then, place your setup on a sheet of paper, and trace both the light rays and the edge of your lens.

Then, repeat with the diverging lens (the one that looks like someone took a brick and pinched the middle).

Part V: (Not Part of Lab) Forming Images Via Lenses, (left click to expand)

Warning: Excel/Sheets/etc.'s trig functions assume inputs of radians, and the inverse trig functions output angles in radians. Pay attention to this when doing calculations involving trigonometric functions.

Part I: Refraction

First, calculate angles \(C\), \(D\), and \(E\). For simplicity, here are the formulas for them (although you should verify that they are true):

$$C=A-D\label{C}$$ $$D=\tan^{-1}\left(X_1/Y_1\right)\label{D}$$ $$E=\tan^{-1}\left(X_2/Y_2\right)\label{E}$$

Then, calculate the sines of these angles (and \(A\)). Keep in mind (for both of these calculations) the warning above.

Note that, for both of these steps, we did the uncertainty propagation for you (because propagating uncertainty through trigonometric formulas is somewhat messy and uses specialized formulas that require calculus to motivate).

Then, using those sines, calculate the index of refraction, assuming \(n_\text{air}=1\), twice, once at each boundary (i.e., once using angles A and C, and once using angles D and E).

Finally, answer the questions on the data sheet about whether these agree with the expected value for \(n\).

Part II: External Reflection

Answer the questions about whether your results agree/make sense.

Part III: Total Internal Reflection

Calculate the sine of the critical angle (as above, keep in mind the warning, and the trig error propagation is done for you).

From this, calculate index of refraction, and propagate uncertainty.

Then, answer the questions about whether your results agree/make sense.

Part IV: Parallel Rays Into Lenses

For the diverging lens, on the diagram you traced, project the lines backwards: take a straightedge, and draw a dashed line going backwards from each outgoing light ray.

On each ray tracing diagram, circle the focal point of the lens (on the relevant side of the lens). Measure the distance from the center of the lens to the focal point, and record this (with appropriate sign, and with uncertainty, which may be large!) as your focal length.

Answer all questions on the data sheet.

Part V: (Optional) Forming Images Via Lenses, (left click to expand)

Your TA will ask you to answer some of the following questions (they will tell you which ones to answer):

Experimental Questions:

1. Suppose you had some random error in \(X_1\) or \(Y_1\). Would this error have a same-direction or opposite-direction impact on angles \(C\) and \(D\)? A same-direction or opposite-direction impact on your two measurements of \(n\) in part IA? Suppose we got a measurement of \(n\) by averaging the two measurements we got in this part. Would you consider this feature of our errors to be a good thing or a bad thing from the perspective of getting an accurate measurement of \(n\), and why?
2. How could we perform part III of this experiment by measuring only distances? (There are multiple potential answers here; come up with a set of measurements you think are plausible to perform, physically speaking, and a formula relating them to your conclusion. Show your work.)
3. Qualitatively, what would you expect to be the result of a lens that is not "thin"? (Would the rays be deflected more or less than otherwise?)

Theoretical Questions:

1. Show that formulas \eqref{C}-\eqref{E} are true.

For Further Thought:

1. The Earth's ionosphere has an index of refraction less than 1 (due to it being a plasma). Draw what a radio wave passing from the Earth's atmosphere (with \(n=1\) into the ionosphere above might look like, based on Snell's law, for a large angle w.r.t. the relevant normal. (Hint: it's going from an area of larger index of refraction to one of smaller index of refraction... what can happen in such a case?) How might this aid long-distance radio transmission?

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)