
Ohm's Law
In this lab, we will use measurements to determine whether various circuit components (a resistor, light bulb, and diode) follow Ohm's law, V=IR.Hoveroverthese!
- 1 DC Power Supply
- 1 Voltmeter
- 1 Ammeter
- 1 Resistor Board
- 5 Banana Cables
- 4 Alligator Clips
- Record data in this Google Sheets data table

Resistors
The voltage across a resistor is determined by the current flowing through it and a property of the resistor known as the resistance using Ohm's Law:1
$$V=IR\label{Ohm}$$In general, circuit components for which this property are called Ohmic. It is possible to have something which acts "like" a resistor, in the sense that voltage is dependent on current through it, but the resistance depends on voltage; such components are called non-Ohmic.
In reality, like Hooke's law, "being Ohmic" is always an approximation that is only valid over a certain range, in this case a certain range of voltages. Nevertheless, the range is sufficiently large, for appropriate components, that the approximation is often useful.
In general (to an appropriate approximation), the resistance of a (cylindrical) resistor is determined by the length of the resistor \(L\), the cross-sectional area \(A\), and the "resistivity" \(\rho\):
$$R=\frac{L\rho}{A}$$The resistivity \(\rho\) is not a property of the geometric shape of the resistor, just of the material the resistor is made from. However, it can be influenced by the thermodynamic state of the material (i.e., the temperature, pressure, etc. of the material). This can be important if your temperature changes significantly (as it does in, e.g., a light bulb, which has the filament become very hot in order to glow).
Diodes
An interesting non-Ohmic component is a diode. An ideal diode acts like a "one-way infinite resistor": one way, no current passes through (so we say it has "infinite" resistance in that direction); in the other direction, it has no resistance (so it's like it's not even there).
A more realistic diode has a resistance which varies exponentially with voltage. This makes it so a small "forward" voltage causes the resistance to decay to almost zero, whereas a small "backward" voltage causes the resistance to explode to infinity. This is concisely represented by the Shockley diode equation:
$$I=I_S\left(e^{\frac{V}{nV_T}}-1\right)$$Here, there are a few constants characterizing the diode, but the most important one is \(V_T\), the thermal voltage. This is ~26mV at room temperature, hence much smaller than the voltages we will deal with in this lab. The others are \(n\simeq 1\), known as the quality factor, and \(I_S\), known as the saturation current.
When we go backwards with a large voltage, \(V\ll -V_T\), we have the exponential being approximately zero, hence our current becomes an (approximately constant) \(-I_S\). We then have a measurement of resistance that looks like \(R\simeq\frac{|V|}{I_S}\rightarrow \infty\) as \(V\rightarrow -\infty\).
Conversely, when we go forwards with a large voltage, we can neglect the \(-1\), and so the current grows exponentially with voltage. Practically speaking, this means that other resistances in the circuit are more likely to determine the resistance and limit the current. Thus, in the limit of large voltage (compared to the very-small \(V_T\)), we can (relatively speaking) neglect the voltage across the diode.
Click here for advice on NOT burning out the fuse in your ammeter.
If you wire your circuits hastily, you may accidentally damage your equipment - in particular, you may burn out the fuse on the front of your ammeter. That's a fixable issue (talk to your TA), but it's still a waste of time and equipment, so here is best practice for wiring to avoid shorting out fuses in the ammeters:
- Before you wire up your circuit, turn off the power supply, voltmeter, and ammeter. Turn the voltage knobs on the power supply all the way down.
- Wire up your circuit. Double-check your wiring, to be sure. The most important thing is to make sure there is no route from the positive end to the negative end of the power supply which doesn't have a resistor (or voltmeter) along the way; note the diode does not count.
- Turn on the instruments. Set the voltmeter to its max setting, and the ammeter to its second-highest setting (as the 5A setting requires using the other port).
- Turn up the voltage on the power supply to something reasonable - say, middle position (on the "coarse" knob, if you have a three-knob power supply).
- Turn down the voltmeter/ammeter settings to the smallest number which is still larger than the given voltage/current. This ensures that you maximize your precision while not overloading your device.
- Finally, note that, as you take measurements, you should adjust the voltmeter/ammeter settings so that they are always the smallest number larger than the measured voltage/current. As the numbers change, your settings should, too.
The simpler power supplies only have one knob, which will be what you control your voltage with in this experiment. There are also three-knob power supplies, which are not much more complicated, but you have to know what knob does what.
Click here if you have a three-knob power supply.
First, turn the rightmost knob ("Current") all the way to maximum, and leave it like this for the rest of the experiment. The switch on the upper-right doesn't matter.
You'll be working with the other two knobs, which adjust voltage. The left knob is a "coarse" adjustment (to get you to the right ballpark), and the right knob is a "fine" adjustment (to tweak the voltage output). Use accordingly.
All voltages should be read off the digital voltmeter, not the analog display on the power supply.
Part I: Measuring the Resistance of a Single Resistor
Over the course of the lab, your TA will be going around measuring resistances of your resistors with a multimeter (or they may be provided ahead of time).
First, choose a resistor to measure. Read the resistor code (the colors on the side of the resistor), and record the resistance. Also record the value measured with a multimeter.
Click here for instructions on how to read resistor codes.
The resistors we use in this lab are typical axial-lead, carbon resistors rated to 1/4 Watt maximum power. The resistance value and tolerances of the component are noted with colored stripes ("bands") to a standard which is nearly 100 years old Wikipedia on Resistors
To read the code, note that these are 4 Band resistors. The metallic band (Gold or Silver) indicates the tolerance and is the last band, usually separated from the others. Look at the resistor with the metallic band last (to the right). Note the colors of the other bands from left to right and record them in your data sheet.
To interpret the code and get your resistor value, note that each color corresponds to a digit 0-9. Bands 1 and 2 form a 2-digit number (ie. Red-Red means 22, Brown-Black means 10, Yellow-Violet means 47). Band 3 gives a multiplier (ie. Red means 102, Brown means 101). The resistor value is the product of the 2-digit number and the multipler (ie. Red-Red-Brown means 22x101=220 Ohms). Internet resources to help you are plentiful; this article from Arrow Electronics is a good one.
Then, wire the circuit up as shown below:2

Click here for step-by-step instructions for setting up your circuit for Part I.
Assuming you are starting with no wires connected:
- Begin by wiring a red wire from the red terminal on the power supply to the right (250mA max) terminal on the ammeter. (Note: if your current goes over 250mA during this experiment, you will need to change ports.)
- Connect the center (COM) terminal on the ammeter to the right-hand side of the resistor you're using (R1 or R2 on the board), using an alligator clip to attach to the resistor.
- Using a black wire, connect the left-hand side of the resistor you're using to the black terminal on the power supply (again using an alligator clip).
You should now have a loop that goes from your power supply, through your ammeter, through the resistor, and back to the power supply.
- Connect a red wire from the positive (red) terminal on the voltmeter to the right-hand side of the resistor using a new alligator clip.
- Connect a black wire from the negative (black) terminal on the voltmeter to the left-hand side of the resistor using another new alligator clip.
You should now have made a second loop that runs through your voltmeter instead of through the resistor. This completes the necessary wiring for this part.
Once everything is wired up, set your power supply to 1V or so. Measure voltage and current.
Slowly turn up your voltage to 10V in units of 1V (again, approximately). Measure voltage and current at each step.
Now, we want to also test negative input voltages to our resistor. The easiest way to do this is to flip the wires at your power supply (so red is wired to black and vice versa).
Part II: Light Bulb
Replace the resistor with the light bulb in your circuit, and swap the power supply back to "normal."
Set your power supply to 5V or so; your light bulb should now light up. If it does not, consult your TA.
Now, turn your voltage down low, where the bulb does not light up (much). Take ten measurements of current and voltage between 0V and 2V.
Flip your orientation (as before), and take ten measurements between -2V to 0V.
Part III: Diode (Optional)
Revert the power supply back to "normal." We'll now be dealing with the diode+resistor combination; note that you should only hook the power supply up to the ends of this combination, not the middle peg. (The middle peg can short out your ammeter!)
The following diagram shows you (in terms of the physical appearance of the diode) which way current is "allowed" through the diode.
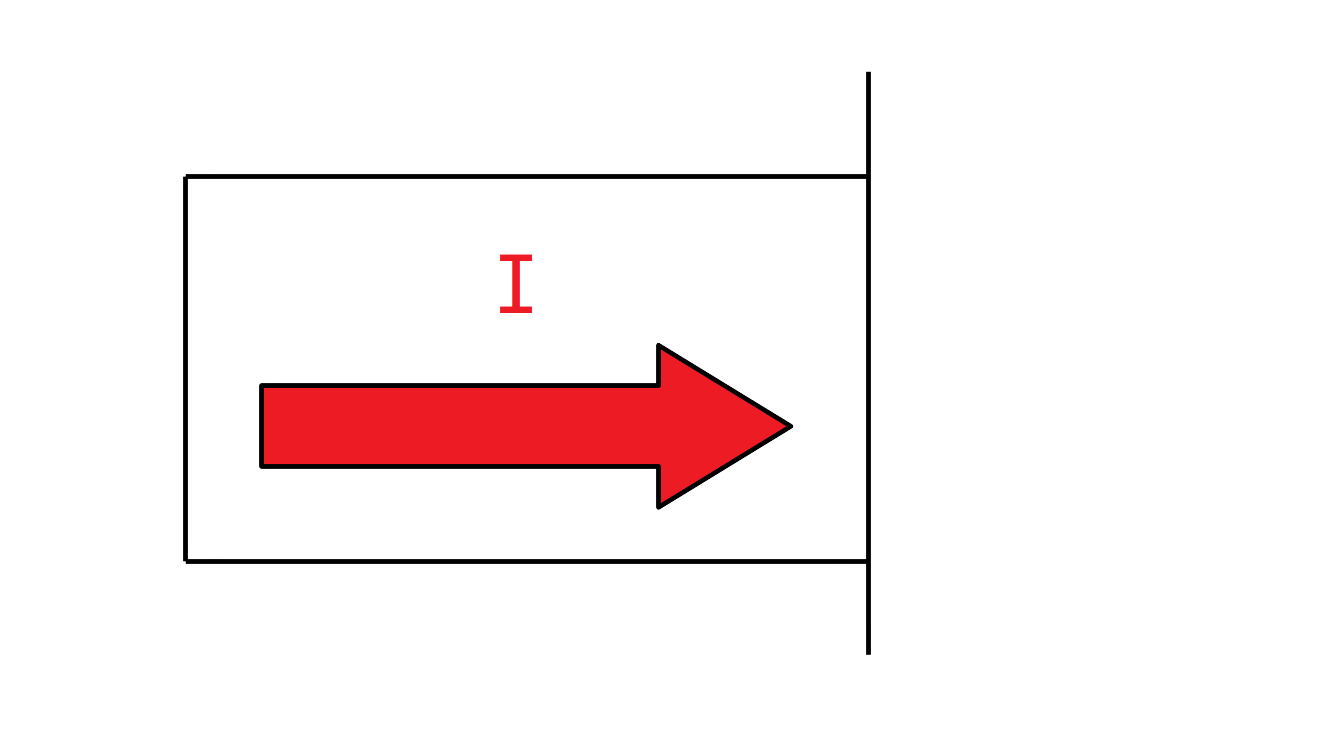
(towards the end with the flat disk)
In accordance with that picture, connect the "high" (red) end of the power supply to the tail of this arrow, and the "low" end of the power supply to the head (on the two ends of the diode-resistor pair - again, nothing to the middle peg). However, some boards have a diode which conducts in the opposite direction! Use the hand-drawn arrows on the board as a guide.
Set your power supply to 1V, and check that you get a nonzero current. Then, take ten measurements of voltage and current from 0-10V.
Swap the direction of the power supply, and take 0V to -10V. (Are your results the same?)
Finally, using the color bands (as in Part I), record the resistance of the resistor (i.e., without the diode) on your data sheet.
Part I: Resistor
Make a plot of voltage vs. current. We violate the usual convention for such plots here, which would be to put the independent variable (voltage) on the x-axis and the dependent variable, current, on the y-axis. We do this, simply put, to make the analysis easier.
Determine the resistance (and uncertainty) based on this plot. Answer the question on the data sheet about whether your result agreed with expectation.
Part II: Light Bulb
Make a plot of voltage vs. current for the light bulb, without a best fit line. Look at the qualitative behavior of this plot.
If your data is linear with no intercept (as you should have obseved in part I), then the light bulb acts like an ohmic resistor (voltage is directly proportional to current). If not, then the resistance depends on the current.
State your results on your data sheet by answering the stated questions.
Part III: Diode (Optional)
As with the previous two circuit components, make a current vs. voltage plot, again without a best fit line. Is it linear? What does ths imply about whether or not the diode is ohmic (overall; i.e., with both directions considered together)?
Now, the "wrong" direction behavior should be pretty clear just by looking at your data; let's look at the "right" direction behavior (where you see nonnegligible currents). Make a separate current vs. voltage plot for just this part of your data, and add a best fit line this time.
From this second plot, calculate the resistance of the resistor+diode combination. Is this compatible with the expected resistance in this direction? (Consider what the diode's resistance in the "forward direction" should be, and how the the resistances of the diode and resistor combine in series.)
Your TA will ask you to discuss some of the following points (they will tell you which ones to answer):
Non-ideal Voltmeter/Ammeter: In this experiment, we make an assumption of an "ideal voltmeter" with infinite resistance, and an "ideal ammeter" with zero resistance. Let's see what happens if we don't make this assumption.
Suppose our components were non-ideal: suppose the ammeter instead had a small (say, 3Ω) resistance \(R_A\), and the voltmeter had a large but still finite (say, 1MΩ) resistance \(R_V\). These resistances can be incorporated by making the following replacements in the relevant circuit diagrams:

Discussion: Non-ideal measurements I.e.: a realistic voltmeter is actually more like a combination of an ideal voltmeter and a large resistor in parallel; a realistic ammeter is more like a combination of an ideal ammeter and a small resistor in series. (In other words, our "better assumption" is just that the voltmeter accurately measures the voltage across it and that the ammeter accurately measures the current through it.)
- Impact of Non-Ideal Components: Draw the new circuit diagram with the non-ideal voltmeter and ammeter. If we take the voltage across the voltmeter and divide by the current through the ammeter (as, effectively, was our procedure in this experiment), what resistance do we expect to actually measure? Does the voltmeter's non-infinite resistance cause a systemic error here? Does the ammeter's non-zero resistance?
- Alternative Wiring: Suppose now that we had used instead a slightly different wiring setup, where the voltmeter was instead wired across both the ammeter and resistor (instead of just across the resistor). Draw the new circuit diagram, first with an ideal voltmeter/ammeter and then assuming they are realistic (with the above replacements). Now, what resistance do we actually measure? Again, does the voltmeter's non-infinite resistance cause a systemic error here? Does the ammeter's non-zero resistance?
- Comparison of Alternative Wiring: Take your resistor's listed value for Part I, and compute the "actual" measured resistance for each wiring setup (the one we used, and the one we didn't), assuming the values for \(R_A\) and \(R_V\) suggested above. For which one is the measured resistance closer to the resistance we want to measure?
- Analyzing the Light Bulb: You should have noticed that the light bulb doesn't have a single well-defined "resistance," since the current vs. voltage plot is nonlinear. Nevertheless, one can define a "voltage-dependent resistance" as \(R(V)=\frac{V}{I(V)}\) as the ratio of voltage to current.1
- Basic Behavior: According to your data, does this resistance increase or decrease with voltage? A reasonable (and correct) thought is that the impact is really with temperature, as the light bulb heats up with more power going into it. How does your data imply resistance varies with temperature?
- Thermal Expansion: One hypothesis you might have is that the reason is that the resistor expands slightly with increased temperature (since most materials do), and hence the cross-sectional area and length of the resistor change. Supposing the resistor increases in size by the same factor in every direction, what direction does the resistance change? (I.e., does the resistance get larger or smaller?) Is this the direction that you expect based on your answer to the previous part?2
- Resistivity Changes: Another hypothesis would be that the resistivity itself changes with temperature. In order to understand why, we need a model of resistivity; one often-used simple model is the Drude model,3 wherein the resistivity can be calculated as \(\rho=\frac{m}{nq^2\tau}\). Clearly, neither the mass \(m\) nor charge \(q\) of the electron will depend on temperature. Thus, for the resistivity to vary with temperature, either the number density of "conduction electrons," \(n\), or the time between electron collisions with ions, \(\tau\), will change with temperature. What is a plausible reason that one of these factors might change with temperature? Does the direction of that change result in a change in resistivity that matches what you expect? (I.e.: would the temperature-dependent effect you note cause the resistance to increase or decrease? Does that match what you expect?)
- Diode Circuit: Why do we do this extra work of adding a resistor to the diode circuit, then subtracting it out? Why do we not just measure voltage and current across the diode alone to measure its resistance?
- Four-Point Resistance Measurement: In our circuitry directions, we advised using new alligator clips for each connection (in particular, when you connect the voltmeter), rather than "stacking" banana cables into each other. This helps to reduce a problem known as contact resistance: there is some resistance in the connection between the alligator clips and the resistors. Why would using more alligator clips help this problem? (Hint: draw out the circuit diagram with both configurations, with this "contact resistance" in the appropriate place in the circuit for each configuration. Then, remember: in some places, extra resistance is problematic; in other places, it is not.)43
Hovering over these bubbles will make a footnote pop up. Gray footnotes are citations and links to outside references.
Blue footnotes are discussions of general physics material that would break up the flow of explanation to include directly. These can be important subtleties, advanced material, historical asides, hints for questions, etc.
Yellow footnotes are details about experimental procedure or analysis. These can be reminders about how to use equipment, explanations of how to get good results, troubleshooting tips, or clarifications on details of frequent confusion.
For more information about Ohm's Law, see Katz 28.6 or Giancoli 25.3. For more description of circuitry in general, see Katz, Chapter 29 or Ginacoli, Chapter 26.
Credit for the right diagram in this manual goes to past student Marina Niazi.
For more information on the Drude model, a good starting point is Hyperphysics from Georgia State Univ.
This is an example of a four-point resistance measurement, albeit one that's not really necessary.
One can also define a differential resistance as \(\frac{1}{R}=\frac{dI(V)}{dV}\), but this will have similar behavior here. (In general, both can be separately interesting in nonlinear circuit components; only in Ohmic resistors are they always equal.)
Now, realistically speaking, relative size changes due to thermal expansion are very small, so regardless of your conclusion about which direction this impacts things, the results are smaller than relevant anyway.
Realistically, this isn't within our precision to measure unless there is a lot of contact resistance, but the principle stands.