In this lab, we will observe the force that a magnetic field exerts on both currents and on free charges.

In the first part, we will measure the deflection of a hanging wire as a function of current through the wire to measure the strength of a magnetic field through which the wire hangs.

In the second part, we will measure the radius of the path of a free electron flying through a magnetic field. In so doing, we will measure the charge-to-mass ratio of the electron, \(e/m\).^{Hoveroverthese!}

• 1 Magnetic Force Apparatus
• 1 DC Power Supply (with current readout)
• 1 20g mass
• 1 e/m apparatus consisting of:
  • 1 set of Helmholtz coils (wires & mount)
  • 2 DC power supplies (one for current in coils, one for accelerating voltage)
  • 1 vacuum tube (with some low-pressure Helium gas)
  • 1 electron gun
• 1 light-blocking hood
• Record data in this Google Sheets data table

General Theory of Magnetic Forces

In general, magnetic forces are governed by the magnetic field, \(\vec{B}\).¹ Like the electric field, the magnetic field is a vector associated with every point in space, although it has some different properties (whereas electric fields go from positive charges to negative ones without loops, magnetic fields tend to loop around currents).

If we have a free charge \(q\) moving through this magnetic field with velocity \(v\), and the angle between \(\vec{v}\) and \(\vec{B}\) is \(\theta\), then the magnitude of the force on the charge is:

$$|F_B|=|q|vB\sin(\theta)$$

The direction of this force is perpendicular to both \(\vec{v}\) and \(\vec{B}\), as given by the right-hand rule.¹

For a current \(I\) (which consists of many moving charges), we replace \(|q|v\) with \(IL\). Here, \(L\) is the total length of wire in the magnetic field \(B\).² Thus, the force law in this case is:

$$|F_B|=|q|vB\sin(\theta)$$

Similar to the above, the direction of the force is perpendicular to the current (i.e., to the wire itself) and to the magnetic field, again in accordance with the right-hand rule.²

Creation of Magnetic Fields

There will be two different sources of magnetic fields in this lab: permanent magnets, and loops of wire (specifically, a Helmholtz coil).

In the first part, we will be using permanent magnets. They are placed south-pole-to-north-pole with a small distance between them (through which we will thread a wire). The magnetic field is then approximately some constant strength \(B\) between the magets and approximately \(0\) outside of them.

In the second part, we will be using loops of wire to make our magnetic field. If we place a single loop of wire in the plane \(z=z_0\) and measure the magnetic field at some other point \(z\) (along the axis of the center of the loop), we get a magnetic field strength of:

$$B=\frac{\mu_0}{2}\frac{Ia^2}{((z-z_0)^2+a^2)^{3/2}}\label{1loop}$$

Here, \(a\) is the radius of the loop, \(I\) is the current through the loop, and \(\mu_0\) is the permeability of free space.

Our apparatus will be a bit more advanced than this: we will place \(N\) loops of wire at \(z=+a/2\), and another \(N\) loops of wire at \(z=-a/2\). This configuration is known as a Helmholtz coil.³ If we now consider the magnetic field halfway in between, we find that the magnetic field strength is:

$$B=\frac{8}{5\sqrt{5}}\frac{\mu_0 NI}{R}\label{BHH}$$

Part I Setup: Magnetic Force on a Wire

In this part of the lab, we will hang a wire through a magnet (with known tension in the wire) and measure its deflection, thereby determining the strength of the magnetic field of the magnet. Our apparatus is represented by the following schematic:

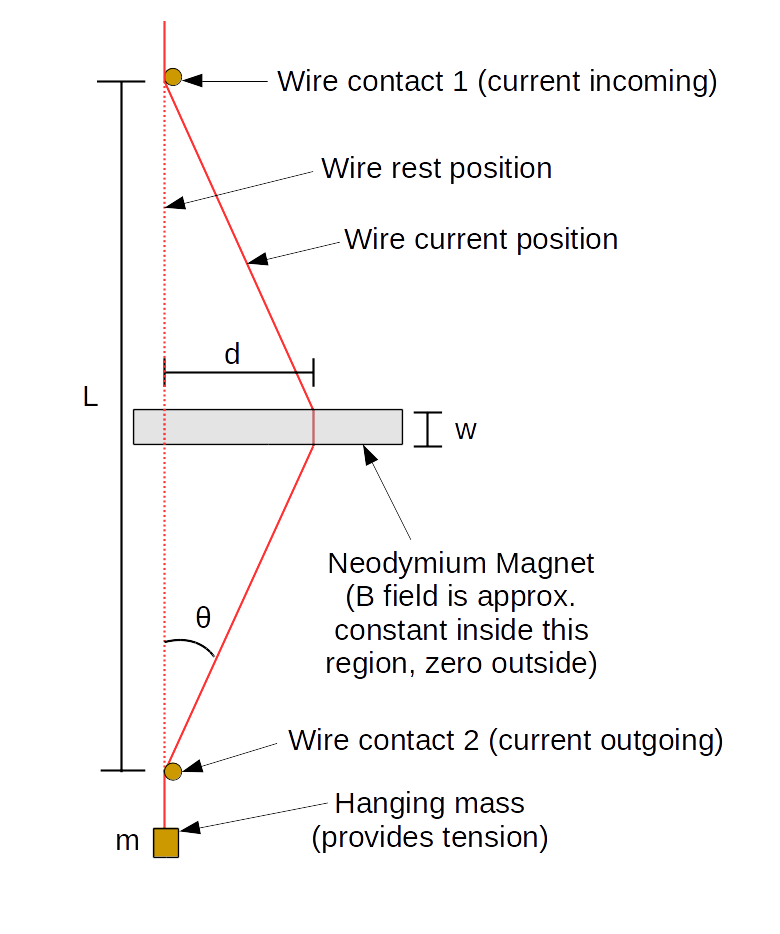
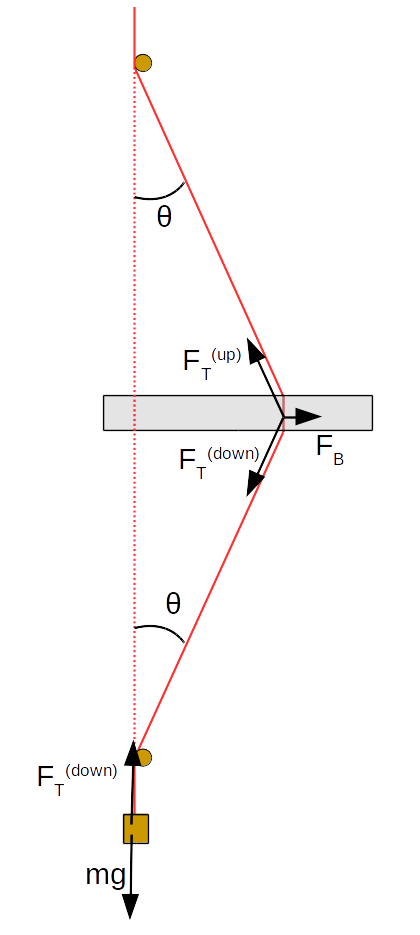
Note that the magnets are located approximately halfway down the wire, such that \(L/2\) length of the wire is above and \(L/2\) is below. This makes the angle at the top equal to the angle at the bottom.

Since this angle is small in this experiment (so \(\sin(\theta)\simeq\tan(\theta)\)), we make the approximation that the length of the diagonal is fixed at \(L/2\) (rather than half the vertical). This allows us to derive a simple relationship between \(d\) and \(B\):³

$$d=\frac{LF_B}{4mg}=\frac{LwB}{4mg}I\label{dformula}$$

In fact, we will measure the horizontal position \(x\), where \(d=x-x_0\) (for \(x_0\) some rest position we don't care about), which obeys the equation:

$$x=\frac{LwB}{4mg}I+x_0$$

Part II Setup: Magnetic Force on a Charge

In the second part of this lab, we will be firing electrons through a magnetic field. Free charges moving perpendicular to a magnetic field move in circles, since they experience a force perpendicular to their velocity. Using the equation for centripetal force,⁴ \(F_C=\frac{mv^2}{r}\), and the equation for force on a moving charge (where \(\vec{v}\perp\vec{B}\)), we get the equation:

$$\frac{mv^2}{r}=evB\label{forces}$$

The electron's speed is determined by the electron source. The electrons are essentially "dropped" through a voltage \(V\), so that they are ejected with energy \(eV\). Hence, we also know:

$$eV=\frac{1}{2}mv^2\label{energies}$$

Combining these two equations and doing some algebra reveals a formula for the charge-to-mass ratio of the electron:

$$\frac{e}{m}=\frac{2V}{(Br)^2}\label{em}$$

Now: our magnetic field is produced by a Helmholtz coil with \(N=130\) turns, where each loop has a known current \(I\). Since \(B\) is proportional to \(I\), and we know (and vary) \(I\), we can write our magnetic field as:

$$B=\alpha I$$

(This will conveniently separate the quantity we will change, \(I\), from the quantities that remain fixed throughout our experiment.)

Using equation \eqref{BHH} above, we can compute \(\alpha\):

$$\alpha=\frac{8}{5\sqrt{5}}\frac{\mu_0 N}{R}$$

Plugging this into equation \eqref{em} and rearranging, we find our final relationship that we will plot:

$$V=\frac{\alpha^2}{2}\left(\frac{e}{m}\right)(Ir)^2$$

This experiment takes place in two parts, with two distinct setups. You will switch setups halfway through the experiment. This may require waiting for a group on the other setup to finish.

The setup for Part I looks like a giant wooden tower and an associated power supply. The setup for Part II looks like two coils with a glass sphere in the center on a metal platform.

Part I: Magnetic Force on a Current

We'll begin by taking some preliminary measurements of the dimensions of the device itself.

Using a meter stick, measure the distance \(L\) from the bottom contact (higher of the two at the bottom) to the top contact. You may take \(w\) as given as 0.50" (the dimensions of the magnet are 0.50"x0.50"x2.00"), and convert that to SI units, or you can measure it yourself with a meter stick to the best of your ability.

Now we will set up our power supply. This takes a little effort, because of how this supply works: it is both voltage and current-limited.⁴ In other words, you set a maximum voltage \(V_{max}\) and a maximum current \(I_{max}\), and the power supply outputs the largest voltage/current that it can without exceeding either of those limits.

For our purposes, we want to use the current knobs to set the current, and just make sure the voltage is "high enough." To do that, perform the following procedure:

1. Turn all knobs all the way to the left (so we start with no outputs). Then turn the voltage knob back up just a little.
2. Plug a wire directly from the red port of the power supply to the black port of the power supply. (I.e., make a short circuit, meaning we will be "current-limited," since any voltage will make a large current.)
3. Turn up the "coarse" current knob a little bit (a quarter-turn). The "current" light should be on (since we are current-limited).
4. Next, disconnect the short-circuit, so that nothing is plugged in. (We are now back to being "voltage-limited," because we can set an arbitrary voltage without running into the current limit - since, of course, no current will be output when disconnected.)
5. Now, turn the voltage knob up until it reads somewhere around 5-6V. (This is large enough to output all currents we expect to use in our experiment. However, imposing the limit ensures that even if you accidentally set the current too high, you won't vaporize the thin wire, because the voltage will still be limited.) The "voltage" light should now be on.
6. Finally, turn the current knobs all the way down again; now you're set up. (Leave the voltage knobs as they are for the rest of the experiment.)

Now, plug in your power supply to your setup (red to red and black to black). We will now be operating in "current-limited" mode, so by varying the current knobs will simply vary the current directly (with no practical complications from voltage).

With that done, the setup is more-or-less out of the way; let's move to considering the actual measurements.

First, hang your 20g mass from the bottom of your hanging wire. (Be gentle - the wires are very thin and fragile!) Drape the wire through the contacts at the bottom, so it passes between them, touching both.¹

Now, take a measurement of your \(x\) position at zero current. This is your first data point.

Slowly increase the current to a maximum of 4.0A in increments of 0.5A, and record the current and position at each step.

Ensure as you do so that your wire does not have significant friction with either the front or back of the display.²

After you hit the end (at the maximum current), bring it back down to 0A again, also in 0.5A increments, and record the positions again. (This helps average out any friction present: if friction "drags down" on the way up, then it "drags up" on the way back down.)

Finally, take note of which direction the current runs along the wire (which we will use to determine the direction of the magnetic field of the magnet).

Part II: Magnetic Force on Free Charges

Next, plug in and turn on your machine. Wait the 30 seconds it takes to boot up. Drape the hood over the top of the machine, if it is not there already.

Turn your voltage and current knobs until you see a green circle of light illustrating the electron beam. This circle may be dim, so look closely! It is easiest to see where it crosses the measuring rod in the center.³

Now: let's figure out which direction the magnetic field from the Helmholtz coil points. We will deduce this from how the electrons move.

One fact you need to know about the machine's setup to make this deduction: the electrons in the electron beam travel in a clockwise direction, when the machine is viewed from the front (i.e., from the side with the digital displays). [Note: this is talking about the electrons in the illuminated green beam, not the electrons in the loops of wire.]

Next, figure out the direction of the magnetic force on the beam. (Remember that the magnetic force in this setup is providing the centripetal force that keeps the beam going in a circle - what direction does centripetal force always point?)

From the force and the velocity of the electrons (and knowing that the electron charge is negative), deduce the direction of the magnetic field of your apparatus, using the right-hand rule. Additionally, knowing this magnetic field, deduce which direction the current in the coils is travelling (using the right-hand rule for the production of magnetic fields).

Once you know what direction the magnetic field of your apparatus points, you can align your apparatus. Rotate it (if needed) so that the magnetic field of the apparatus is perpendicular to magnetic North.

A few notes on how to do that. The building is more-or-less aligned with the cardinal directions, with one wall marked as true N. You should first align your compass rose so that N on the compass rose points to true north. Then, the compass rose will give you the direction of magnetic North/South, which of course is aligned with the Earth's magnetic field (neglecting vertical components).

Once you aligned your apparatus, it is time to take measurements. Choose a value for current, and adjust your voltage until the beam is centered on the smallest marker. The marker tells you the diameter, in cm; record the diameter, the current, and the voltage (with associated uncertainties).

Then, increase the voltage until you hit the next marker, and again record the same quantities. Repeat until you hit the largest marker.

Then, choose another value for current, and repeat the process (again, for a variety of radii). You can stop when you get sufficiently many data points.

Part I: Magnetic Force on a Current

Make a plot of \(x\) vs. \(I\), and from the slope, calculate \(B\). Propagate all relevant uncertainties, and compare to the expected value of B=0.35±0.05T. (The relatively large uncertainty accounts for variation in magnet strength from setup to setup.)

Then, deduce the direction of the magnetic field of the magnet from the current direction and the deflection direction.

Part II: Magnetic Force on Free Charges

First, from coil diameter, calculate coil radius, \(a\). Then, calculate \(\alpha\) and its uncertainty.

For each data point, calculate \(r\) from beam diameter, then calculate \((Ir)^2\). Propagate uncertainties.

Finally, make a plot of \(V\) vs. \((Ir)^2\). From the slope and your calculation of \(\alpha\), determine a measurement of \(e/m\), the charge-to-mass ratio of the electron.

Your TA will ask you to answer some of the following questions (they will tell you which ones to answer):

Experimental Questions:

1. Consider your magnetic field measurement in Part I. How does it compare to the strength of the Earth's magnetic field? To the strongest magnetic field created on Earth? To a typical MRI machine? Which one is it closest to (in scale)?
2. Compute the magnetic field of the Helmholtz Coil for a typical current value in Part II (say, for a 1A current). Consider the strength of the Earth's field, by comparison. Suppose we hadn't taken care to orient our apparatus perpendicular to the Earth's field. How much of an effect would you expect the Earth's field to have?⁵
3. In Part II, at the edges of the coil, the deviations of the magnetic field from the value at the center is approximately 7%. How does this compare to the other uncertainties you have in this lab?
4. Why is it far easier to measure \(e/m\) experimentally than either \(e\) or \(m\) individually (not just with this experiment, but with any setup)? Note: "the numbers involved are small" is not a complete answer; while that has elements of the truth, there's a deeper reason that you should get at.

Theoretical Questions:

1. Show that equation \eqref{dformula} holds, starting from the force diagrams provided above. (Remember that you have to make the approximation that the diagonal is \(L/2\) rather than \(\sqrt{(L/2)^2+d^2}\) in order to have that formula hold exactly.)
2. Find the exact equivalent of \eqref{dformula} - i.e., find the formula relating \(d\) and \(I\) without making the approximation that the angle is small.
3. Derive formula \eqref{em}: first, explain why formulas \eqref{forces} and \eqref{energies} must hold. Then, do what algebra is necessary to show that those formulas imply formula \eqref{em}.
4. Derive formula \eqref{BHH}: starting from formula \eqref{1loop}, show that equation \eqref{BHH} holds. (Hint: you can just add the fields of each set of \(N\) loops separately, one set of loops at \(z_0=+a/2\) and the other at \(z_0=-a/2\).)

For Further Thought:

1. What level of precision in position would we need (order-of-magnitude) to measure the magnetic field of the earth? (Look up the magnetic field of the Earth, and see what \(d\) would be in such a case.) Is it plausible to have this level of precision, given reasonable instrumentation? Why/how?
2. For Part II, we're running many experiments at the same time in the same room; we should consider: can the magnetic field of the coil across the table from you impact your experiment? Suppose you have another setup 1m away, and pretend it is just 260 loops of wire (along the z-axis) with 1A of current. Take formula \eqref{1loop}, multiply by \(2N\) to account for all the loops, and plug in 1m for \(z-z_0\) (and then the other parameters as usual) in order to compute the magnetic field in your coil that is actually made by the coil across the table from you. How does this compare to the magnetic field your own coil makes (at its center)? To Earth's field?

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

Plotting Tool