In this lab, we will observe the force that a magnetic field exerts on a current.

By measuring this force, we will measure the strength of the underlying magnetic field.^{Hoveroverthese!}

• 1 Magnetic Force Apparatus
• 1 DC Power Supply (with current readout)
• 10g and 20g masses
• Record data in this Google Sheets data table

The magnitude of the force on a wire in a magnetic field is:¹

$$\vec{F}_B=I\vec{l}\times\vec{B}$$

In this lab, we will be using a special case of this (for when the magnetic field and wire are orthogonal):

$$F_B=|\vec{F}_B|=IlB$$

In this lab, you will be working with an apparatus represented by the following schematic:

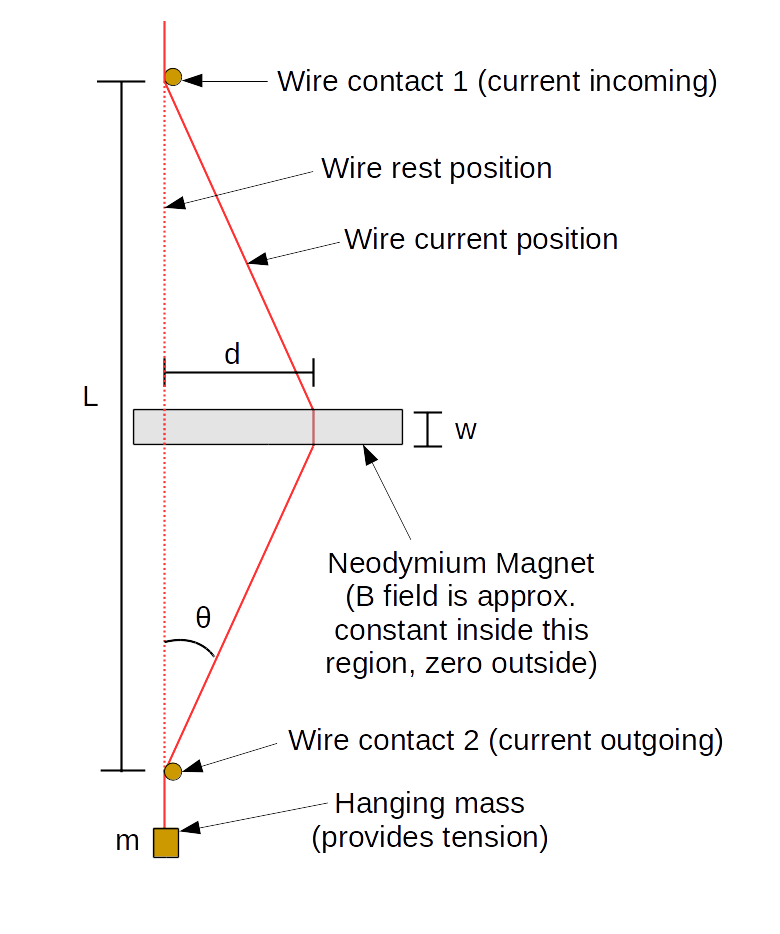
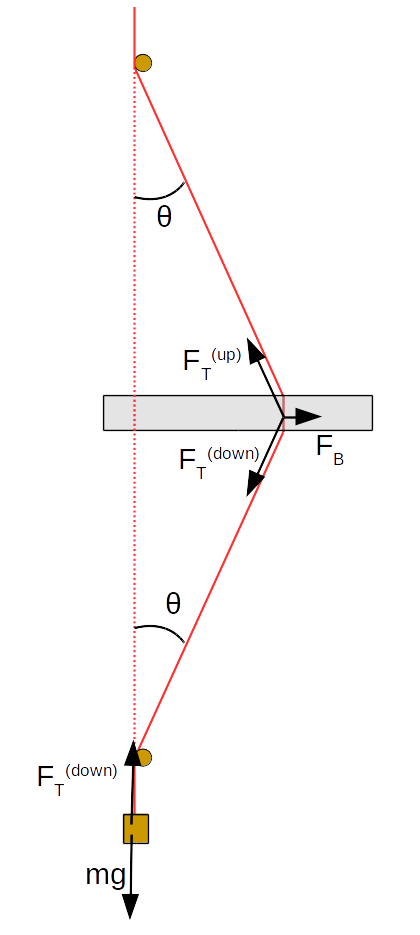
Note that the magnets are located approximately halfway down the wire, such that \(L/2\) length of the wire is above and \(L/2\) is below. This makes the angle at the top equal to the angle at the bottom.

Since this angle is small in this experiment (so \(\sin(\theta)\simeq\tan(\theta)\)), we make the approximation that the length of the diagonal is fixed at \(L/2\) (rather than half the vertical), which allows us to derive a simple relationship between \(d\) and \(B\):

$$d=\frac{LF_B}{4mg}=\frac{LwB}{4mg}I\label{dformula}$$

In fact, we will measure the horizontal position \(x\), where \(d=x-x_0\) (for \(x_0\) some rest position we don't care about), which obeys the equation:

$$x=\frac{LwB}{4mg}I+x_0$$

Preliminary Measurements

Using a meter stick, measure the distance \(L\) from the bottom contact (higher of the two at the bottom) to the top contact.

You may take \(w\) as given as 0.50" (the dimensions of the magnet are 0.50"x0.50"x2.00"), and convert that to SI units, or you can measure it yourself with a meter stick to the best of your ability.

Setting Up the Power Supply

First, set all knobs on your power supply all the way to the left.

Plug a wire directly from the red port of the power supply to the black port of the power supply. (Make a short circuit.)

Turn up the "coarse" current knob a little bit (a quarter-turn). Then, disconnect all wires.

Now, turn the voltage knob up until it reads somewhere in the range of 2-4V.

Turn the current knob all the way down again, and then you're set up. (Leave the voltage knobs as they are for the rest of the experiment.)¹

Now, plug in your power supply to your setup (red to red and black to black).

20g Mass Measurements

Hang a 20g mass to the bottom of your hanging wire. (Be gentle - the wires are very thin and fragile!)

Drape this wire through the contacts at the bottom, so it passes between them, touching both.

Do not loop it around either contact. If your wire is too long and your mass is resting on the bottom of the apparatus, tie a knot higher up in the wire to hang from (or consult your TA).

Now, take a measurement of your \(x\) position at zero current. This is your first data point.

Slowly increase the current to a maximum of 4.0A in increments of 0.66A, and record the current and position at each step.

Ensure as you do so that your wire does not have significant friction with either the front or back of the display.¹

After you hit the end (at the maximum current), bring it back down to 0A again, also in 0.66A increments, and record the positions again.

10g Mass Measurements

Hang the other mass now, and do the exact same measurements as the previous part. Only two modifications are needed.

First, take increments of 0.5A instead of 0.66A. This will ensure you get enough data, due to the next instruction.

With the lighter mass, you will find that you reach the end of the position scale before you reach 4.0A. This is fine; just stop once you do so (and do not record any data with the wire in contact with the right-hand side of the apparatus), and go back down from there.

For each mass, make a plot of \(x\) vs. \(I\), and from the slope, calculate \(B\).² Propagate all relevant uncertainties.

On the data table, state whether your results for the two masses agree with each other.

Your TA will ask you to answer some of the following questions (they will tell you which ones to answer):

Experimental Questions:

1. Which mass' B field measurement do you think is more reliable? (Consider in particular the sensitivity to outside forces.)
2. What level of precision in position would we need (order-of-magnitude) to measure the magnetic field of the earth? (Look up the magnetic field of the Earth, and see what \(d\) would be in such a case.) Is it plausible to have this level of precision, given reasonable instrumentation? Why/how?

Theoretical Questions:

1. Show that equation \eqref{dformula} holds, starting from the force diagrams provided above. (Remember that you have to make the approximation that the diagonal is \(L/2\) rather than \(\sqrt{(L/2)^2+d^2}\) in order to have that formula hold exactly.)
2. Find the exact equivalent of \eqref{dformula} - i.e., find the formula relating \(d\) and \(I\) without making the approximation that the angle is small.

For Further Thought:

1. Look up the strength of the magnetic field of Earth: how does the magnet we have in this lab compare? How about to the strongest magnetic field ever made in a lab? Which is it closer to (in scale)?²

Guide to Uncertainty Propagation & Error Analysis

Plotting Tool