
Interference & Polarization
In the first part of this lab, we will qualitatively look at the interference pattern of a diffraction grating.
In the second part of this lab, we will observe diffraction by a human hair, and use it to measure the width of that hair.
In the third part of this lab, we will look at the behavior of linearly polarized light.Hoveroverthese!
- 1 Helium-Neon Laser (632.8nm)
- 1 Micrometer (small-distance-measuring device)
- 1 Frame (+ tape)
- Hair (yours)
- Movable wall
- 2 LED flashlights
- Wave Optics Slides:
- 2 Diffraction Gratings (500 lines/mm, 1000 lines/mm) ["rainbow" version]
- 3 Polarizers
- Cornell slides (a few per room) & lamp
- Record data in this Google Sheets data table
General Wave Optics
There are three "simplest" optical components from which one can consider interference: a single slit, a pair of slits, and a diffraction grating (many slits, equally spaced).1
The setup is virtually identical for all three components: you have some source of light shining on your component. We suppose this source of light releases a uniform collection of light that is in phase with itself, meaning the "maximum" of the wave is the same for every position in the direction perpendicular to the light's travel.
The light then collides with the component, which only lets light through from certain positions. Per Huygen's principle,2 we can consider each of these to be a source of light separately, and see how the outcomes on the right-hand side interfere.
We will observe some maxima and minima, and we want to know (in terms of the wavelength of the light, \(\lambda\), and the parameters of the component the light passes through) where these maxima/minima are.2
Ultimately (after some work), we find that these maxima/minima occur at certain fixed angles away from "straight ahead."
These angles can be calculated (in all the scenarios we are interested in this lab) with a single equation:
$$m\lambda=b\sin(\theta_m)\label{DiffFormula1}$$The quantities vary slightly between the different setups:
- For a single slit of width \(b\), \(\theta_m\) is the angle of the \(m\)th minima (from the center).
- For a pair of (perfectly-thin) slits of separation distance \(b\), \(\theta_m\) is the angle of the \(m\)th maxima.
- For a diffraction grating with a separation distance \(b\) between each slit and the next, \(\theta_m\) is the angle of the \(m\)th maxima.
Important for this lab: we treat a thin "blockade" (like our human hair) as essentially equivalent to a single thin slit.1
Suppose the light ultimately shines on some plane (i.e., we project the output light on a wall). The angle \(\theta_m\) can now be expressed in terms of the distance \(d\) of the minimum/maximum from the peak and the distance \(D\) between the component (slit/grating) and the wall:
$$\tan(\theta_m)=\frac{d_m}{D}$$We now make an approximation that the angle \(\theta_m\) is "small," allowing us to approximate \(\sin(\theta)\simeq\tan(\theta)\). Under this approximation, we get the resulting equation:
$$m\lambda=b\frac{d_m}{D}$$Solving for the quantity we are interested in, \(d_m\), we then get:
$$d_m=\frac{\lambda D}{b}m\label{DiffFormula2}$$Measurements of Diffraction in This Experiment
We use diffraction in two ways in this lab, which superficially seem different, but are really the same.
First, we "project" the diffraction pattern on a wall with a laser. In this setup, the pattern forms in the following way:

Second, we see the diffraction pattern as a set of virtual images of the LED, seen through the diffraction grating. This is illustrated in the following diagram:
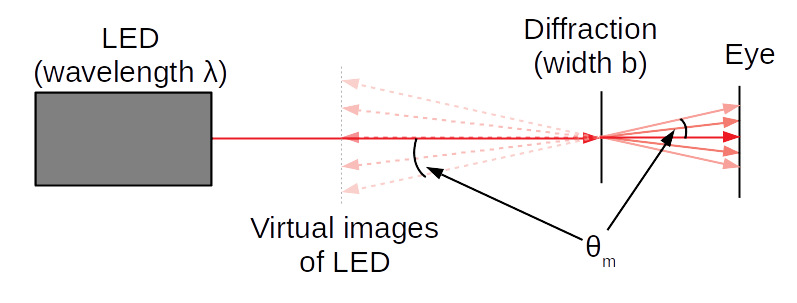
Note that in the latter case, the "real" angles are the ones we see in the eye (since that's the diffraction of the actual laser beams), but it looks like the laser is "behind" the diffraction grating at exactly the same angle. Hence, we can treat the angle we see the (virtual) image at as a measurement of the angle of diffraction.
Two Slits of Nonzero Width
Now let us consider a somewhat more complicated scenario, less ideal than the previous cases. Suppose instead of one of the above components, we instead shine our light source on two slits of nonzero width.
We only discussed the maxima and minima, not the intensity, but fortunately, we don't need an explicit formula to understand what is going on (as much as we need to). We just want to understand the qualitative behavior of the intensity's dependence on angle, \(I(\theta)\).
Suppose your intensity of light at some angle \(\theta\) is measured by some function \(I_1(\theta;b_1)\) for one slit of width \(b_1\), and \(I_2(\theta,b_2)\) for a pair of infinitely-thin slits with separation distance \(b_2\).
The full intensity function is then given by:
$$I(\theta)=I_1(\theta;b_1)I_2(\theta;b_2)$$Let us suppose that the slits are notably thinner than the distance between them. Then, the oscillations in \(I_1\) will be have a much larger "period" than the oscillations in \(I_2\).
In other words, in this supposition, one-slit diffraction would give long bright patches (with occasional fringes), and two-slit diffraction would give rapidly changing bright and dark patches.
The net combination of these effects is a rapid oscillation in brightness (from the two-slit separation) which eventually goes entirely dark after some distance (when \(I_1=0\)), then comes back for a second set of oscillations, etc.
Babinet's Principle (Diffraction by a Hair)
A human hair is not, itself, a single slit. However, we are allowed to treat it as such using an idea known as Babinet's principle.
Suppose we have two patterns which are complementary, in the sense that one pattern is opaque where the other is transparent, and vice versa. (An example would be our hair and a slit of the same width in an otherwise-opaque wall.)
If there were no barricade, our light would make a "straight-forward" pattern. Call the resulting output beam \(E_0\) (\(E\) for electric field, since light is an oscillating electric (electromagnetic) field).
Let's say that if we put our first pattern, we get some output beam \(E_1\), and for our second pattern, we get some output beam \(E_2\).
Now, we make an appeal to intuition. Because all the light for \(E_0\) must go through either the transparent part of the first pattern or of the second pattern,3 we must have that the two patterns add up to the total: $$E_0=E_1+E_2$$
Note that, aside from directly ahead of the beam, \(E_0\) is zero. Therefore, away from the original beam:
$$E_1=-E_2$$Light intensity is proportional to the magnitude of the electric field oscillation squared. Hence, away from the original beam, we have Babinet's principle:
$$I_1=I_2$$This allows us to conclude that we can treat the human hair the same as a single slit (so in particular it has the same minima), provided we only look at the space "outside" the original laser beam.
Polarization of Light
We know that light is an oscillating electromagnetic field.4 Let's focus on the "electric" part. There's a natural question to ask: what direction does the electric field oscillate?
A basic principle is that the electric field always oscillates perpendicularly to the direction of propagation of the light.3 There are still, however, two directions in which the electric field can be oscillating.
Supposing the light is moving in the z-direction, a general oscillation will be a combination of oscillations in the x and y directions, potentially with a phase shift between them. This results in the general "motion" of the electric field (in the plane perpendicular to the motion of the light) being an ellipse of some sort.
There are certain special cases that are interesting to consider. If light has purely vertical oscillations, we call it vertically polarized; if purely horizontal, horizontally polarized. If the light has oscillations purely in any one direction (along any axis - some line of oscillation instead of an ellipse), we more generally call it linearly polarized.
Even if the light is not purely linearly polarized, it can still be partially polarized. For instance, suppose it oscillates in an elongated ellipse that mostly goes in the y-direction, but a little in the x-direction. We could call this "partially vertically polarized." By contrast, if the magnitude of the oscillation doesn't depend on direction, we call the light unpolarized.
One can make polarized light in a variety of ways,4 but the most common (and simplest) is to use a linear polarizer. This is a material that lets through light of one (linear) polarization but not the other, and is the component we use in this lab.
For instance: if you have a polarizer in the vertical direction, only the y-component of the light passes through, and you end up with vertically polarized light which is (if the light is not initially vertically polarized) less intense than the initial beam (since you only took one component of that beam).
Circular Polarization (not used in this lab)
Another special case of interest is when the ellipse is actually a circle, known as circularly polarized light. Since there are two directions the electric field could be spinning around zero (while remaining in the plane perpendicular to the light's motion), there are two cases: "left-handed circular polarization" and "right-handed circular polarization."
Similar to how a general wave can be written in terms of x and y parts, a general wave can also be written in terms of left-handed and right-handed parts (again, potentially with a relative phase shift). In many areas of physics, this is a much more natural way to understand the "components" of light.
One nice property is that it doesn't refer to x and y axes explicitly (except in the definition of what our "relative phase shift" means). Aside from knowing the direction of linear (or elliptical, i.e., partial-linear) polarization, we know everything from just "how much" of each circular polarization we have.
Circular polarizations also have a specific angular momentum: left-circularly polarized light has angular momentum in the direction of the light's motion, and right-circularly polarized light has angular momentum against the light's motion. This can make it useful to analyze systems where angular momentum is "interesting," such as electrons making transitions between atomic energy levels of known angular momentum (i.e., known quantum number \(l\) and/or \(m_l\)).
Part I: Qualitative Interference Behavior
Seeing the Diffraction Pattern:
Look through the 500 lines/mm diffraction grating at the red LED1. You should see the LED in the center, but also - if you look off to the left and right - horizontal red lines, which are the "diffracted" images of the LED. Observe this pattern.
Now, look at the blue LED simultaneously (through the same grating). How does the distance from the center to the "diffracted images" compare for the two different colors?
Now, just look at the red LED. Compare the 500 lines/mm grating to the 1000 lines/mm grating. How do they compare? Which has a larger distance?
Diffraction by a Laser:
Finally, turn on your laser. Put the "movable wall" a short distance (~10-20cm) away, and point the laser at it.
Put either diffraction grating in front of the laser. You should see the diffraction of the beam nice and clear - a few nice, bright spots off to the side!2
Move the wall closer to and further from the laser. As you move the wall closer to the laser, do the dots get closer together or further apart?
Qualitative Observation of One-Slit and Two-Slit Interference Patterns with Cornell Slides (not required)
Somewhere in the room should be a large "lamp box" with blue and red filters on it, along with a few "slides" of various slits.5
The slides have many features; we will just look at a few. Look down the left-hand slide (with the words at the top of the slide the right way around): you should observe a series of single slits, of varying widths.
Look through them at the filament of the lamp. You should see some lines that are the same shape as the filament, right adjacent to it.
Vary which slit you look through. How do your observations of these lines change as the slit width varies?
Now, on the right-hand side, you should observe pairs of slits, of constant width but varying separation. If you look through them, you should observe a "beat pattern": bundles of close-together-lines that have some larger-scale pattern.
Vary the slit separation. What happens to the larger-scale pattern? To the smaller-scale pattern? What does this tell you?
Part II: Diffraction by a Human Hair
Take a hair from your head (or - with permission - someone else's head, if you don't have the hair for it yourself).
Direct Measurement of Hair Thickness:
The first thing we will do is measure the thickness of this hair using a micrometer.
Click here to learn how to use a micrometer.
For the most part, the micrometer looks like an adjustable wrench. The outer part of the handle spins, and as it does, you make (or close) a gap in the circular part.
To take a measurement, you first put the thing you want to measure in the part that closes, and then clamp the micrometer shut (but not too hard).
You then need to read the numbers. Some of the numbers are on the inner part of the handle; for our micrometer, each mark is 1mm (as you should be able to see). However, hairs aren't mms thick, so you won't need this for our experiment.
Instead, you'll just be looking at the numbers on the "spinning" part of the handle (that range from 0 to 50). Each one of these ticks is 10μm (0.01mm). You determine which one you are reading by seeing which tick mark lines up with the line on the not-spinning part of the handle.
(Similar to a meter stick, you can read to less than a tick mark, and for optimal attempted precision, you should do so.)
It is entirely possible that, for your "zero point measurement" (see below), you will end up reading something like 47 (so 470μm). In this case, this is really three less than zero (since "0" looks the same as "50"), so you can just mark it as -3 (i.e., -30μm).
Begin by setting your micrometer closed with nothing in it. Don't squeeze it, just set it closed (and remember the degree of "firmness" with which you closed it - when you put the hair inside, you want about the same level of "firmness").
Ideally, it would be reading zero, but unfortunately, it probably isn't (due to imperfect calibration). Record this "zero-measurement" (with uncertainty).
Now, put the hair inside, and shut it on the hair (again, don't squeeze). Take the reading of the micrometer with the hair inside (with uncertainty). Although "zero" may not be quite right, the difference between our "with-hair" measurement and our "zero" measurement should still be (approximately) the width of the hair.
Observation: Diffraction by the Micrometer (not required)
Note that the smallest marker on the micrometer (0.01mm) is only one order of magnitude greater than the wavelength of visible light.
You might call it a single slit, and this is qualitatively correct, but is complicated by the fact that the inside edges of the grating are "shiny." This makes interference with the reflected rays as well (since we're essentially looking through a "thin slit" with walls made of mirrors).
If you want to see it yourself, here's something you can try. Go into the hallway outside the lab and look up at one of the (relatively) long, thin tubes in the lights on the ceiling. Hold the micrometer close to one of your eyes so that you're looking through a, say, 0.1 mm gap directly at a fluorescent tube “lengthwise”.
If you carefully orient the micrometer gap, you will both directly see the lamp and an image of it reflected off the shiny faces that delimit the gap. Adjust your "aim" so that the images coincide. Now, without moving the "aim" too much, close the gap.
At some closure you'll start to see whitish and blackish "bands," and their thickness and separation will vary with the width of the gap. This pattern is too complicated to understand without great care. However, if you keep closing the gap, at about 0.05 mm, you should see colors of the rainbow.
This is a clear sign that wavelength-dependent diffraction effects are occurring. See if you notice how the colors separate, and then try to figure out if this is what you would expect for single-slit diffraction. Although you are looking through a deep reflective gap rather than a single slit, maybe what you see is qualitatively similar to what you'd expect for the simpler case of a single slit.
Does the order of colors line up with what you expect? What happens to the colors as you close the gap further?
Measurement of Hair Thickness Using Diffraction:
Now, tape the hair to your frame so that it goes roughly vertically across the hole in the frame.
Set up your screen at the wall side of your lab bench and the laser near the opposite (aisle) side. Place the frame with the hair between the laser and screen, closer (10-20cm, ish) to the laser.
Take note of the wavelength of your laser (which should be written somewhere on it). Then, turn on your laser, and shine it at the hair. Observe that there is a beam spot on the screen and then swing the laser left and right until you see beam spot hit the hair. Now look at the screen: there should be a diffraction. Which way does the diffraction pattern appear (vertical or horizontal)? As you vary the hair's distance from the screen, what happens to the diffraction pattern?
Now: locate the central peak of the difrfraction pattern. You count \(m\) of the dark spots as the \(m\)th spot from the peak (in a particular direction).
Rather than try to locate the "exact" location of the central peak and measure \(d_m\), we'll measure the difference in position between the left \(m\)th spot and the right \(m\)th spot (if you like, between \(m=|m|\) and \(m=-|m|\)), which would be \(2d_m\).
Fix the position of the hair, the laser, and the wall (make sure that the wall is perpendicular to the laser beam). Then, measure the distance \(D\) between the hair and the wall.
Then, measure the distances \(2d_m\) from the left peak to the right peak (it may be helpful to mark all the peaks, and then measure all of them after, when you can take down the wall, with the laser off), up to \(m=5\).
Part III: Polarization
One Polarizer:
First, put a single polarizer in front of the laser. Vary the angle of polarization, and observe the intensity.
Does the intensity vary (significantly) as you rotate it? Is there an angle at which it entirely disappears (or very nearly so)?
What does this mean for the laser light: is it (nearly) completely linearly polarized, partially linearly polarized, or not linearly polarized? If if is linearly polarized (partially or completely), in what direction?
Now, check the LED: by similar logic, is that completely, partially, or not-at-all linearly polarized?
Two Polarizers:
Take two polarizers, and hold them up to some light (the LED will work, or just look at ambient light).
First, put them oriented the same direction: does the light brighten, stay approximately the same, diminish partially, or completely disappear?Now, put the second polarizer perpendicular to the first, and answer the same question.
Finally, put the second polarizer at approximately 45 degree angle relative to the first, and again observe the variation of brightness compared to one polarizer.
Three Polarizers:
Take two polarizers, and put them perpendicular. Then, put the third one in between, at a 45 degree angle from both. What do you observe? (Does this feel strange? After all, on its own, no polarizer will increase the amount of light - they all only let some light through.67)
Now, align the middle polarizer with the first polarizer. What does this do to the light that comes through, compared to 45 degrees? What if you align is with the second polarizer instead?
Part I: Qualitative Interference Behavior
In words, explain your observations from this part in terms of formula \eqref{DiffFormula1} (or, equivalently, \eqref{DiffFormula2}). In particular: explain why the diffraction was larger or smaller in the different cases.
Part II: Diffraction by a Human Hair
Calculate the width of your hair from your micrometer measurements, and propagate uncertainty.
For each \(m\), from \(2d_m\), calculate \(d_m\), and propagate uncertainty. Then, make a plot of \(d_m\) vs. \(m\).
From the slope, extract a measurement of hair diameter, and state whether it agrees with expectation.
Your TA will ask you to answer some of the following questions (they will tell you which ones to answer):
Experimental Questions:
- Look up the range of sizes of a typical human hair8. Do your measurements show that your hair is in this range?
Theoretical Questions:
- Explain why the diffraction pattern of the hair appears in the direction that it does.
- What happens to the image made by a single slit as your slit width becomes very wide? What happens when it becomes narrow (in particular, when \(b<\lambda\))?
- When you take light polarized at some angle \(\theta\) and pass it through a polarizer at angle \(\theta'\), the electric field gets multiplied by \(\cos(\theta-\theta')\), and thus the intensity gets multiplied by \(\cos^2(\theta-\theta')\) (with the outgoing light polarized at angle \(\theta'\)). Using this, explain your results for two and three polarizers for Part III: calculate the expected intensity of the outgoing beam (in each case) in terms of the intensity of the light that makes it through the first polarizer, and relate this to your results.
For Further Thought:
- The photons in a laser tend to be "self-reinforcing": if some of the photons are in one state, the other photons want to be as well. (This is why they can get a relatively narrow range of wavelengths.) Can this intuition also explain our observations about the degree to which laser light is polarized (and if so, how)?
Hovering over these bubbles will make a footnote pop up. Gray footnotes are citations and links to outside references.
Blue footnotes are discussions of general physics material that would break up the flow of explanation to include directly. These can be important subtleties, advanced material, historical asides, hints for questions, etc.
Yellow footnotes are details about experimental procedure or analysis. These can be reminders about how to use equipment, explanations of how to get good results, troubleshooting tips, or clarifications on details of frequent confusion.
For a review of wave optics, review KJF Ch. 17. The simplest case of interference is discussed in Ch. 17.2 (two-slit interference). The scenarios we use in this lab are 17.3 (diffraction grating) and 17.5 (one-slit diffraction).
This principle is discussed in KJF Ch. 17.5.
This is not entirely a true description, even if it is reasonably intuitive. A more proper proof/discussion can be found here.
For more about light as an electromagnetic wave (including more details about polarization), see KJF Ch. 25.6.
The idea that allows us to do this is called Babinet's principle, which says that if we swap what parts of space of light are "blocked" and "unblocked," you get the same brightness pattern (with the exception of the brightness of the "going straight" part of the beam). E.g., by going from a thin slit clear and everything else blocked to a thin blockage with everything else clear, you get the same pattern. For more detail, read below.
For technical reasons, we assume that the distance from the component is "large," much larger than the wavelength of the light or the size of the component, known as the Fraunhofer regime.
The magnetic field oscillates in a direction perpendicular to both the direction of propagation of the light and to the electric field. The basic idea of polarization will therefore apply equally well (since knowing the direction of travel of the light and the electric field tells you the magnetic field), but usually when we say things like "vertically polarized" we are referring to the electric field direction, not the magnetic field direction.
In fact, light is partially polarized even when it just reflects off of something (in general, not requiring any special material). At a particular angle known as Brewster's angle, the reflected ray is completely linearly polarized (in the direction perpendicular to the plane of reflection). As a result, calculating the intensity of reflected/refracted beams is beyond the abilities of ray optics alone.
These slides are called Cornell slides. They were printed at Cornell decades ago, as the thinnest-width slits printable at the time, and a handful were sent out to various universities. Nowadays, they're a bit of a historical relic, but they still work perfectly fine, especially for these purposes!
This is closely related to a fundamental experiment in quantum mechanics known as the Stern-Gerlach experiment. This experiment shows the counterintuitive result that, for a particular set of particle beams, you can add a "barrier" and get more particles out at the end of your beam (analogous to adding our polarizer, which reduces the amount of light, and getting more out). This experiment can also be framed as an interference effect (blocking the "destructively interfering" particle-waves to go from zero to non-zero).
This is also closely related to the counterintuitive fact that sailboats can sail upwind (at an angle). This method is known as tacking. A good explanation of the math behind this is Part II, Problem 3 here (solutions here).
This can vary wildly from individual to individual (with a strong ethnicity dependence, which you may find interesting to investigate if your hair is significantly thicker or thinner than average).
Alternately, shine the LED to the left or right, grazing the (back of) the grating. Try different arrangements until you see the main and diffracted spots.
Nice [optional] things to look at: what happens if you swap which diffraction grating you use? What happens if you use both simultaneously? Does which diffraction grating is in front matter to what you observe, in that case? Why?