In this lab, we will use a diffraction grating to measure the wavelengths of the spectral lines emitted by a tube of atomic hydrogen. Using that information, we will measure the Rydberg constant.^{Hoveroverthese!}

• 1 Hydrogen Gas Tube (light source)
• 1 Diffraction Grating (1000lines/mm, Edmunds Scientific) with holder
• 1 Meter Stick
• 2 Mounted LEDs
• Record data in this Google Sheets data table

Origin of Atomic Spectra

The electrons of atoms have particular configurations that have specific energies. These configurations are known as orbitals.

In general, these orbitals are quite complicated due to electron-electron interactions (among other things). However, when we consider the simplest atom¹ - Hydrogen - with only one electron, the results get quite a bit simpler.

The possible energies of a Hydrogen atom (under certain approximations) are:

$$E_n=-\frac{me^4}{8h^2\epsilon_0^2}\frac{1}{n^2}=-\frac{13.6\text{eV}}{n^2}$$

This is usually measured by observing the energy of transitions between these energy levels. When such a transition occurs, the atom will emit a photon; this photon must have energy equal to the energy of the transition.

Hence, in a transition from energy level \(n\) to energy level \(n'\) (with \(n'\lt n\), such that this is a "downwards" transition), we can write the energy of the emitted photon as the difference between energy levels:

$$E_\gamma=\frac{me^4}{8h^2\epsilon_0^2}\left(\frac{1}{n'^2}-\frac{1}{n^2}\right)$$

Recall also that the photon energy is determined by its frequency, \(E=hf\), and that the frequency is related to the wavelength, \(f=\frac{c}{\lambda}\). Therefore, we can rewrite this in terms of the wavelength:

$$\frac{1}{\lambda_{n\rightarrow n'}}=\frac{me^4}{8h^3c\epsilon_0^2}\left(\frac{1}{n'^2}-\frac{1}{n^2}\right)=R_H\left(\frac{1}{n'^2}-\frac{1}{n^2}\right)\label{Rydberg}$$

This quantity, \(R_H=1.097\times 10^{7}\text{m}^{-1}\), is known as the Rydberg constant.¹

Measurement of Spectra via Diffraction

Recall the formula for the angular location \(\theta_m\) of the \(m\)th diffraction peak for light of wavelength \(\lambda\) passing through a diffraction grating with distance between slits of \(b\):²

$$b\sin(\theta_m)=m\lambda\label{DiffFormula}$$

In this lab, we'll be observing the outgoing lines with our eye, and projecting them backwards onto a ruler to observe the angle of diffraction. (Solid lines are real rays of light, dashed lines are projected "virtual" lines of light - the place where you will see the lines coming from.)

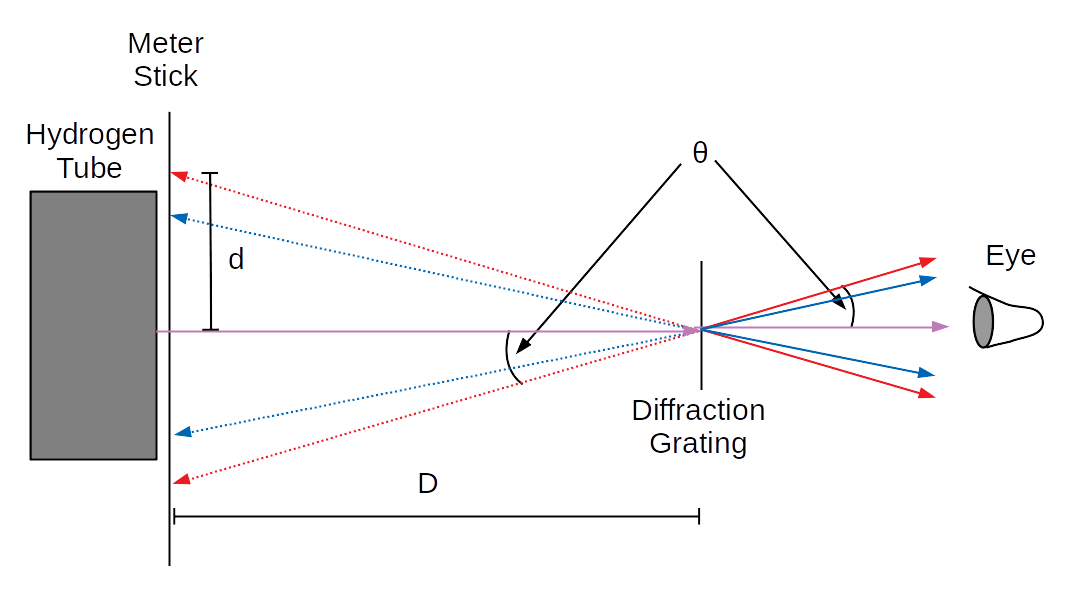
Using some basic trigonometry, we can determine that:

$$\tan(\theta)=\frac{d}{D}$$

By measuring \(d\), we will determine the angle of the \(m=1\) lines, and thereby the wavelength \(\lambda\) of each line.

We will assume that \(n'=2\), and that we are seeing the smallest \(n\) that turn into \(n'=2\) (i.e., \(n=3\), \(n=4\), and \(n=5\)). This will enable us to relate \(\lambda\) to \(n\) and thereby determine the Rydberg constant.

Part I: Qualitative Observations

Plug in your tube and make sure the switch is in the "on" position. Press the button on the handle on the end of the cord; your tube should light up.¹

Put on the diffraction glasses and look at the tube when it is lit up. You should observe a set of colored lines off to the side of the tube (three on either side).²³ The rows of lines above and below the tube you can ignore.²

Hopefully, on the same horizontal axis, you will also observe a second, fainter set of lines, as well; these are the \(m=2\) lines.⁴

Answer the questions on the data sheet about your observations from this part.

Part II: Measurement of the Rydberg Constant

Mount the meter stick on the front of your discharge tube. Put the diffraction grating in the mount, and place the mount about \(40\)cm from the meter stick, oriented facing the tube.

Measure and record the distance between the front of the meter stick and the grating, \(D\). Also note the spacing of the diffraction grating; typically, we use ones that have \(\frac{1}{b}=1000\frac{\text{lines}}{\text{mm}}\), but we also have ones with \(\frac{1}{b}=500\frac{\text{lines}}{\text{mm}}\) and \(\frac{1}{b}=13400\frac{\text{lines}}{\text{in}}\).

We now want to record the location \(x\) of each spectral line (with uncertainties). To do so, we will make use of the LEDs; put one on each side of the meter stick, and turn them on.

Look through the diffraction grating, and line up the LED light with the position of the line.⁵ Do this on both sides simultaneously for one particular color.

Record the position of both the left line and the right line (with uncertainty) for each color. (It is OK if your meter stick moves as you slide around the LEDs, provided both LEDs are in the right place simultaneously for any particular color.)

Part I: Qualitative Interference Behavior

In words, explain your observations from this part in terms of formula \eqref{DiffFormula}.

Part II: Measurement of the Rydberg Constant

First, calculate the distance between lines, \(b\). [We had \(1/b\); note that you do not need to include "lines" in your units on \(b\).]

Figure out (based on knowledge of how color relates to wavelength, and how wavelength relates to \(n\)) which of the lines is \(n=3\), which is \(n=4\), and which is \(n=5\).

For each spectral line, calculate the following:

• The distance \(d\) [as half the separation distance between the two lines], with uncertainty propagated.
• The quantity \(\frac{d}{D}=\tan(\theta)\), with uncertainty propagated.
• The angle \(\theta\) between the tube and the spectral line, then \(\sin(\theta)\). (The Google Sheet will do these uncertainty propagations for you. Remember that Sheets, Excel, etc. do all angle measurements in radians.)
• The wavelength, \(\lambda\), and the inverse wavelength, \(\frac{1}{\lambda}\), with uncertainties
• The quantity \(\frac{1}{n'^2}-\frac{1}{n^2}\) (the right-hand side of equation \eqref{Rydberg}, except for the Rydberg constant)

Make a plot of \(\frac{1}{\lambda}\) vs. \(\frac{1}{n'^2}-\frac{1}{n^2}\). Fit the line through the origin. From the slope, extract the Rydberg constant.

Your TA will ask you to answer some of the following questions (they will tell you which ones to answer):

Experimental Questions:

1. Why do we use \(n'=2\) (known as the Balmer series) in this lab? Why not \(n'=1\) (the Lyman series) or \(n'=3\) (the Paschen series)?
2. Why do we only see \(n=3\) through \(n=5\), and not higher \(n\)?

Theoretical Questions:

1. How would the wavelengths of our lines be modified if we were using Helium instead of Hydrogen? (Assume we are considering once-ionized Helium, so still only one electron.)

For Further Thought:

1. The spectrum described by the Rydberg formula results from taking a Coulomb attraction between an electron and a proton in quantum mechanics. However, there are actually corrections to the Hydrogen spectrum known as fine structure. Look into these corrections: what are the physical reasons behind them? (And why are they small?)
2. Smaller even than the above corrections, one finds hyperfine structure. What is the origin of these corrections? These corrections have a number of applications, including but not limited to:
   • Astronomy: One can locate hydrogen by looking at the very long-wavelength (radio) photons emitted by atoms transitioning between two states which differ in energy by a hyperfine correction. The wavelength of such photons is 21cm; thus, the spectral line is called the 21cm line³.
   • SI Units: We use these corrections to create atomic clocks of very high precision, from which the second is defined (as exactly 9,192,631,770 times the period of a photon emitted in the hyperfine transition of Cs133)⁴.
   • Particle physics: We can make incredibly precise measurements of hyperfine transition frequencies. Being able to compute these frequencies to many decimal places and having these results be consistent with other experiments forms a high-precision test on our knowledge of particle physics.

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

PHY121/122 Plotting Tool