
Conservation of Momentum
In this lab, we will study the principles of conservation of momentum and energy in a variety of collisions.Hoveroverthese!
- 1 Air Track Setup
- 1 Air Track (attached to air pump)
- 1 Large Cart w/ Flag
- 1 Small Cart w/ Flag
- 2x Photogate Setup
- 1 Meter Stick
- Access to a Scale
- Record data in this Google Sheets data table
Suppose you have a cart of mass \(m_1\) and velocity \(v_{1i}\) colliding with a cart of mass \(m_2\) and velocity \(v_{2i}\), with motion confined to one dimension.1
If the collision is perfectly elastic, then both momentum and energy are conserved. In this case, the final velocities of the carts are the following:
$$v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_{1i}+\frac{2m_2}{m_1+m_2}v_{2i}\label{ElasV1}$$ $$v_{2f}=\frac{2m_1}{m_1+m_2}v_{1i}-\frac{m_1-m_2}{m_1+m_2}v_{2i}\label{ElasV2}$$If the collision is totally inelastic, then only momentum is conserved; energy is lost 1. In this case, the carts end moving together with one common final velocity:
$$v_f=\frac{m_1}{m_1+m_2}v_{1i}+\frac{m_2}{m_1+m_2}v_{2i}\label{Inelas}$$In this lab, we will focus on validating the conservation laws themselves (since the above results follow from those conservation laws).
Part I: Preliminary Setup and Measurements
Level your air track, as described in the Air Track Reference Manual (and as you did in the previous lab).
Open the LoggerPro file "ConservationofMomentum" 1 and connect your two photogates, as described in the Photogate Reference Manual.
Measure the mass of both your carts. Measure the width of both carts' flags. Estimate uncertainties in both quantities.
Place the cars on the air track, and the photogates at two different positions along the air track. Ensure that the photogate is high enough that as the carts pass through the photogate, only the flag on top sets off the photogate, not the whole cart.2
Identify which photogate is photogate 1 and which one is photogate 2 by blocking one and seeing which one registers as blocked.
In each of parts II-IV, we will be aligning the air track as follows:
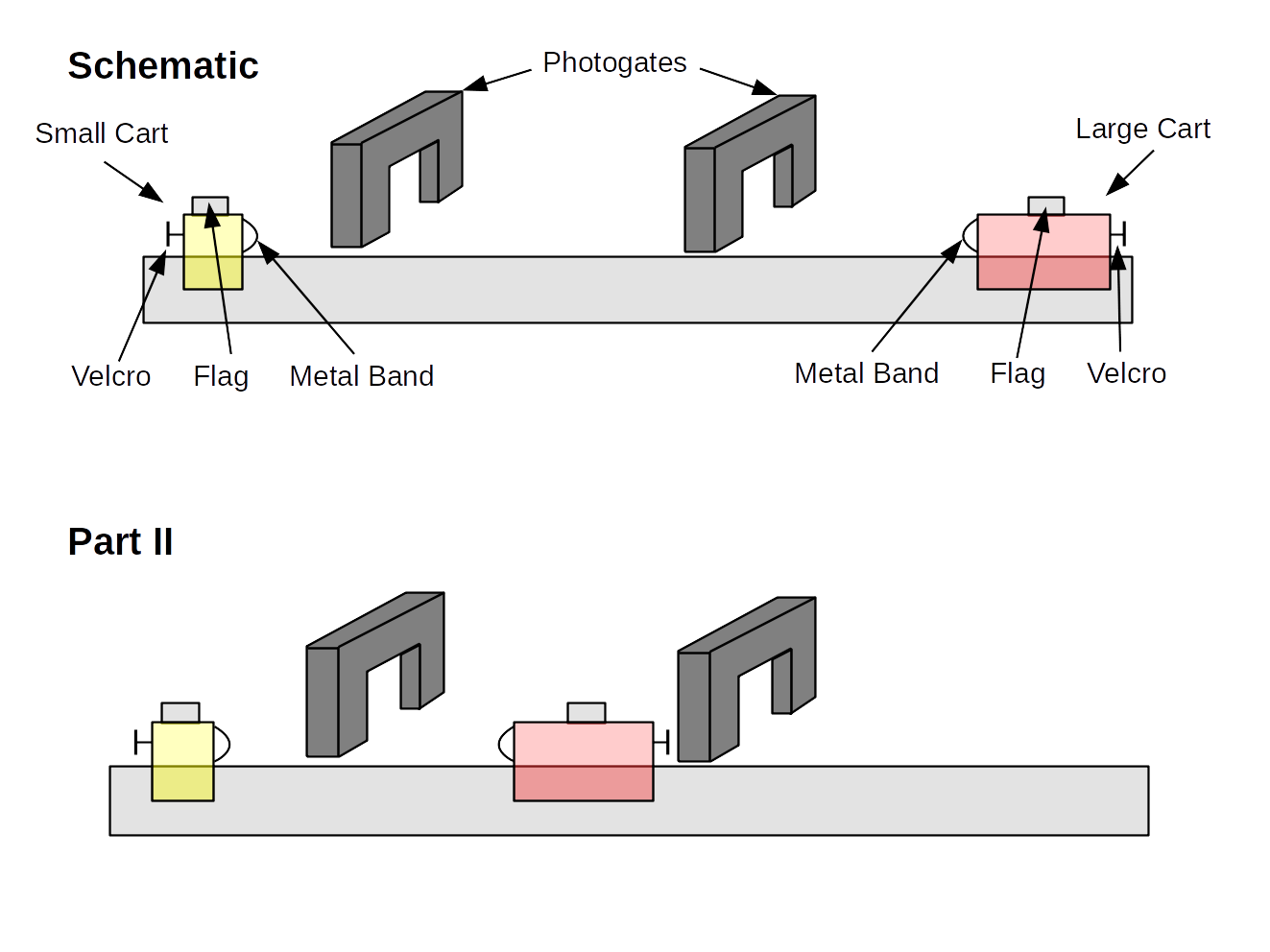
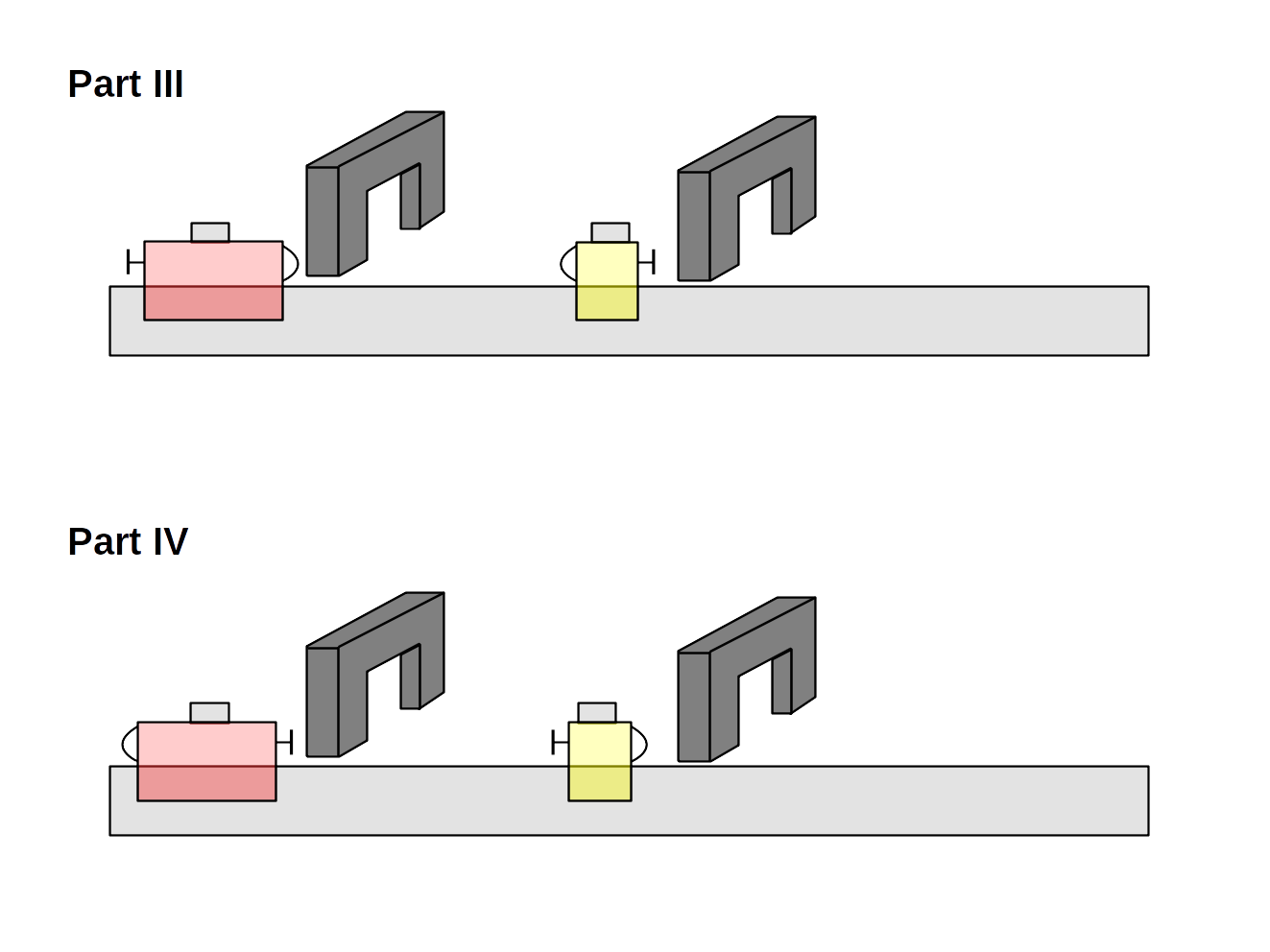
Part II/III/IV: Colliding Two Carts
For each part, do the following:
Set up the two carts and the photogates on the air track as shown in the diagram above.
Press "Start Collection" on the computer, and give the program a second to start recording.
Push the cart outside the photogates lightly (but not too lightly) towards the center. Make sure you are not still pushing it by the time it begins to cross the photogate.
The carts will collide and bounce back. Catch them after they each past the photogate once post-collision.3
The photogates will record a variety of times. They come in pairs: for each photogate, for each cart that crossed in front of it, there is a time when the flag began to cross it and a time when the flag finished crossing it. The difference between these times is \(\delta t\), the time it took the flag to cross it.
Take note of which pairs of times correspond to which crossings of the photogate (knowing which photogate is which should help you here). Record the corresponding differences in times in your data table. Also take note of what directions the carts were moving, initially and finally.
For each collision, do the following:
- Calculate velocity, momentum, and kinetic energy for each cart. Propagate uncertainties.
- Calculate total initial and final momenta and kinetic energies. Propagate uncertainties.
- State whether momentum and energy were conserved, and whether you expected them to be.
Experimental questions:
- How would an unleveled air track impact our conservation of energy and momentum measurements? Does the impact depend on "which way" the track is not level?
- Suppose that the track is bowed; that is to say, the middle of the track is lower than either end. What effects would this have on conservation of momentum in each part? Conservation of energy?
Theoretical questions:
- Show that equations \eqref{ElasV1} and \eqref{ElasV2} result in final velocities conserve both energy and momentum.
- Show that equation \eqref{Inelas} results in a final velocity that conserves momentum.
- Consider the following special cases of collisions. In all cases, a cart of \(m_1\) comes in with a velocity \(v\) and hits a cart \(m_2\) at rest. Most of these are answerable with either intuition or with mathematics. Compute \(\frac{v_1}{v}\) and \(\frac{v_2}{v}\)2 when:
- The collision is elastic, and both carts are the same mass?
- The collision is inelastic, and both carts are the same mass?
- The collision is elastic, and the mass of the first cart is very small compared to the mass of the second cart?
- The collision is inelastic, and the mass of the first cart is very small compared to the mass of the second cart?
- The collision is elastic, and the mass of the first cart is very large compared to the mass of the second cart?
- The collision is inelastic, and the mass of the first cart is very large compared to the mass of the second cart?
- Consider the following special cases of collisions. In all cases, a cart of \(m_1\) comes in with a velocity \(v\) and hits a cart \(m_2\) coming in with velocity \(-v\) (same speed \(v\) from the opposite direction). Most of these are answerable with either intuition or with mathematics. Compute \(\frac{v_1}{v}\) and \(\frac{v_2}{v}\)34 when:
- The collision is elastic, and both carts are the same mass?
- The collision is inelastic, and both carts are the same mass?
- The collision is elastic, and the mass of the first cart is much larger than the mass of the second cart?
- The collision is inelastic, and the mass of the first cart is much larger than the mass of the second cart?
For further thought:
- In the perfectly elastic case, is there another mathematical expression for the velocities that conserves both momentum and energy? If so, what is it, and why do we neglect this possibility? If not, show this (calculate \(v_{1f}\) and \(v_{2f}\) from \(v_{1i}\) and \(v_{2i}\) while making sure you do not have any holes in your argument along the way - e.g., do you ever divide by something that could be zero?).
Hovering over these bubbles will make a footnote pop up. Gray footnotes are citations and links to outside references.
Blue footnotes are discussions of general physics material that would break up the flow of explanation to include directly. These can be important subtleties, advanced material, historical asides, hints for questions, etc.
Yellow footnotes are details about experimental procedure or analysis. These can be reminders about how to use equipment, explanations of how to get good results, or clarifications on details of frequent confusion.
For an understanding of conservation of energy, see KJF ch. 10. For conservation of momentum, see KJF ch. 9. Focus especially on ch. 9.5 and 10.9, which emphasize how these apply to collisions.
The older LoggerPro file "Exp5_t1_t2" will also work.
Beware, in particular, the little screws on top of the cart: if the photogate sees these, you'll get extra times as the screw passes through, which can be confusing.
We want to pretend our air track is infinitely long, without ends; so we don't want them rebounding off the end and colliding again (as the point is that there's no collision with the "outside world," of which the air track end is part!)
That is, some kinetic energy is lost. An aspect of the colision is non-conservative and some energy is converted into thermal energy or another form.
Your answers should not be \(0\) unless the expression is exactly zero. If the answer is "approximately but not exactly" zero, you should be able to calculate that the ratio is approximately a constant multiple of the "small mass over large mass" ratio (\(\frac{m_1}{m_2}\) or \(\frac{m_2}{m_1}\), as appropriate). Other than that, the masses and initial velocity should not appear in your final expression.
Note \(m_1\ll m_2\) is the same as \(m_1\gg m_2\) by symmetry, just in the opposite direction, which is why we don't consider it as another special case.