In this lab, we will study the principle of conservation of energy.

• 1 Air Track Setup
  • 1 Air Track (attached to air pump)
  • 1 Cart w/ Photogate
  • 1 Picket Fence
• 2x 20g Mass
• 1 Meter Stick
• Access to a Scale
• Record data in this Google Sheets data table

In this lab, we will have a mass attached to a string that hangs over a (massless, frictionless) pulley. The other end of the string is attached to a cart on an air track. An air track is like a one-dimensional air-hockey table: it ejects air in order to minimize friction.

In maintaining a nearly frictionless environment, we have isolated our system (to a high degree of precision), meaning energy will be conserved.¹

Schematically, the system is hooked up as follows:

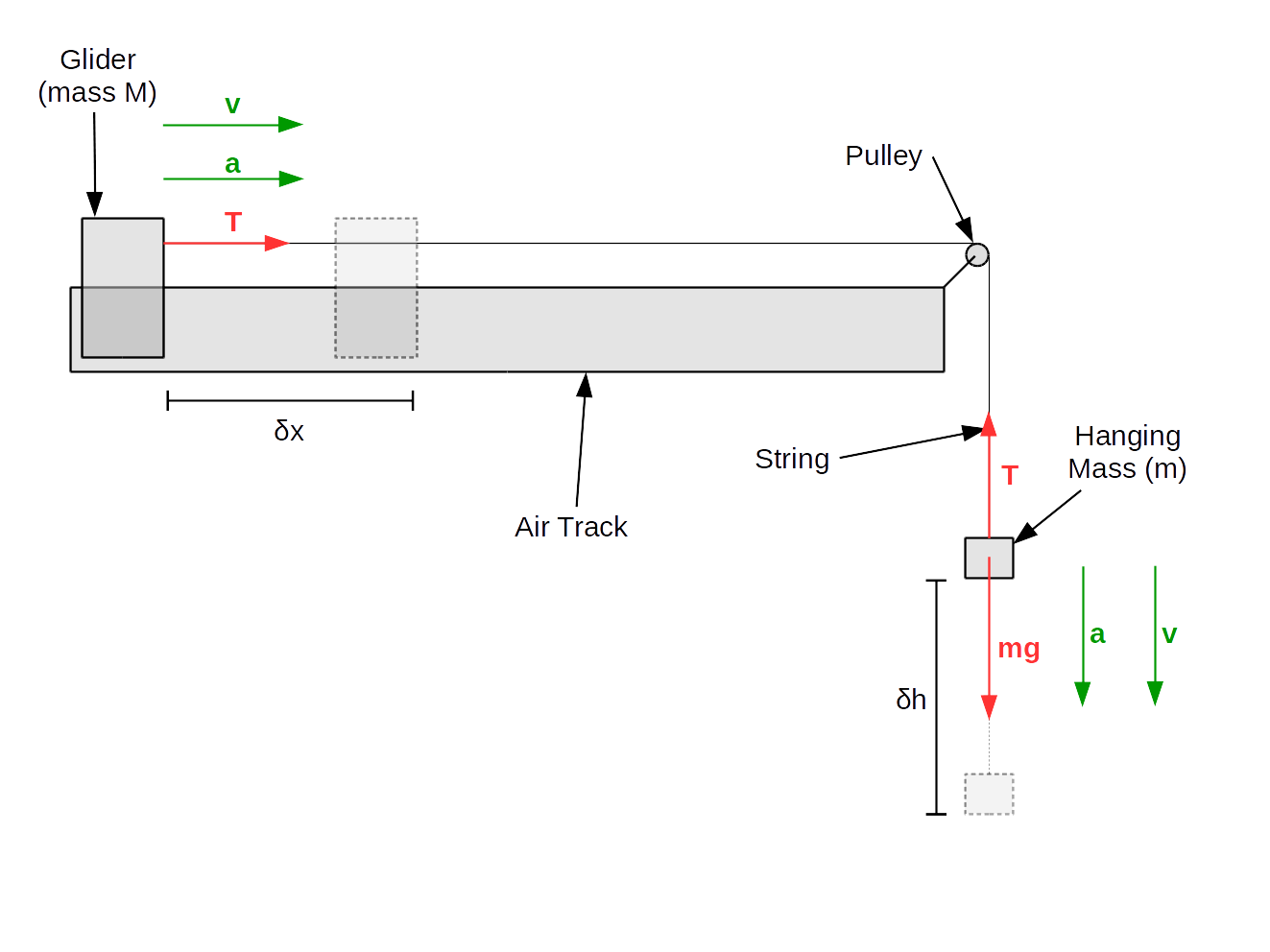
Recall that \(PE=mgh\), so \(\Delta PE=mg\Delta h\). Noting that \(\Delta h=-\Delta x\), we have:

$$\Delta PE=-mg\Delta x$$

Or, more concisely, since "zero potential energy" is arbitrary, we simply assert:

$$PE=-mgx$$

For kinetic energy, we have simply:

$$KE=\frac{1}{2}mv^2+\frac{1}{2}Mv^2=\frac{1}{2}(m+M)v^2$$

The law of conservation of energy states that:

$$E_\text{total}(t)=E_\text{total,initial}\label{ConsEn}$$

Part I: Preliminary Setup and Measurements

Once your TA turns on the air, begin by leveling your air track. Place the cart in the middle of the track, and make sure it doesn't slide to the left or right. If it does, turn the screw on the leg of the air track to adjust the height until the air track is level (in the center).²

Similar to how we did in the acceleration lab, we need to set a scale for the photogate. Measure \(D\), the length of some number of black-clear segments (say, 10), and divide by the number of segments to get \(d\), the length of one segment.

Open "ConservationofEnergy" and ensure your photogate is connected correctly.³.

Weigh your glider¹ to get the mass \(M\). Identify the two masses \(m\) you'll be hanging from the bottom of your string, too.

Hook a string from the glider over the pulley at the end of the air track and down. Ensure that the cart has plenty of space to move before the mass hits the floor.

Part II: Using a 20g Mass

Hook the 20g mass up to the bottom of the string, and pull the cart to the end of the track opposite the pulley.

Press "Start Collection," wait a second, and release the mass. Catch the cart before it reaches the other side, and press "Stop Collection."

Highlight the region of the velocity vs. time plot which is a straight line, and identify which data points that corresponds to.

From the data table, record the time, position and velocity values for the first ten data points of that region. If the region is not long enough, repeat the experiment.

Part III: Using two 20g Masses

Do everything you did in the previous part, except this time with 40g (two 20g masses) instead of 20g hanging off the string.

For each mass, do the following:

• Calculate the weight of the hanging mass, \(F_g\), and the total mass \(m+M\). Propagate uncertainties.
• Convert position and velocity to "physical" units using \(d\). Propagate uncertainty (from \(d\)).
• Calculate PE, KE, and total energy at each time, and propagate uncertainties. (The steps are laid out for you.)
• Make a plot of total energy vs. time (with error bars). Compare the slope to expectation.

Experimental questions:

1. Suppose the pulley has a nonnegligible mass. What effect would this have on the slope of our energy vs. time plot? Why this effect?
2. Suppose the pulley has nonnegligible friction. What effect would this have on the slope of our energy vs. time plot? Why this effect?

Theoretical questions:

1. Let's call the rotational KE of the pulley \(KE_\text{rot}\). In terms of \(KE_\text{rot}\), what is the theoretical relationship between potential energy \(PE\) and translational kinetic energy \(KE_\text{trans}\) if the pulley is massive? (Remember: even when things are spinning, equation \eqref{ConsEn} should still hold if you account for all types of energy.)

For further thought:

1. Let's discuss a nonnegligible mass of the pulley more quantitatively. Take the pulley to have a radius of 4.8cm and a moment of inertia of 11.6gcm\(^2\) ⁴. What is the relationship between \(x\) and \(v^2\) you can write down? You should find \(mgx=\frac{1}{2}(m+M+\mathcal{M})v^2\), for something with mass units \(\mathcal{M}\). We can account for this simply by defining an "effective total mass" as \(m+M+\mathcal{M}\). How big is the extra addition \(\mathcal{M}\) compared to the masses \(M\) and \(m\) we are already dealing with? Is it a relevant systemic error?
2. If you have not, read the question from the Atwoods Machine lab about treating the system as a single "object." The same principle applies here, except that there's no counterbalancing force. Show/explain this.

Guide to Uncertainty Propagation & Error Analysis

PHY121/122 Plotting Tool

Photogate Reference Document

Air Track Reference Document