In this lab, we will study one-dimensional kinematics under constant acceleration.

We will measure the rate of acceleration, which will be the acceleration due to gravity, \(g\).

• 1 Vernier Picket Fence
• 1 Photogate setup
  • Photogate
  • Interface box ("LabPro")
  • Computer
• Record data in this Google Sheets data table

The primary fact we will be using in part I is that the slope of a velocity vs. time graph is acceleration.¹

In part II, we will be using the kinematic equation (in the vertical direction):

$$v_{yf}^2=v_{y0}^2+2a\Delta y\label{vsq}$$

Procedurally speaking, we will be performing this lab using a Photogate.

This device has an LED and a light detector that is able to "see" that LED light precisely when there is nothing in the way of the beam. In this way, it is able to see whether the beam is "blocked" or "unblocked," and measure the times at which this changes.

In this lab, we will be dropping a "picket fence" with black and clear stripes at regular intervals through the photogate, as follows:

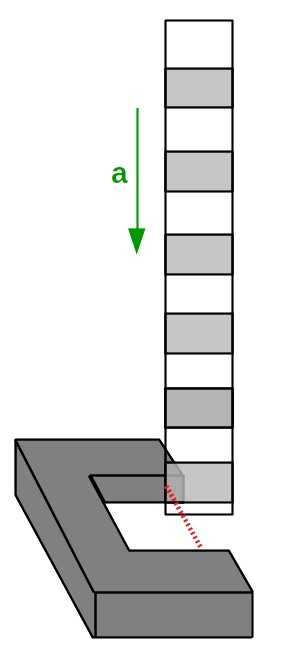
By measuring the length of these strips, we know how far it has fallen whenever it switches from "blocked" to "unblocked" or vice versa. Thus, we will know the y-position at various times, enabling us to understand the kinematics of our system.

Part I: Measuring \(g\) Using a Velocity Vs. Time Graph

First, take your striped plastic rectangle, and measure the distance \(D\) between the bottom of the lowest black stripe and the bottom of the highest black stripe. Estimate your uncertainty in this measurement. Also record how many segments (pairs of black and white stripes) this is.

Turn on the lab computer and log in as "Student" (if necessary). Open the file "Acceleration" in the LoggerPro file folders on the computer. When the window pops up, click "Connect." This should set up the photogate with the computer.¹

At this point, you should be confronted with a screen with three plots on the right and a data table on the left.²

Make sure the photogate is mounted over the floor such that the striped plastic can fall through it when dropped. It may be convenient to put a chair underneath to catch the picket fence (but low enough so that the fence passes all the way through and does not bounce back "in sight" of the photogate).

Hold the fence just above the photogate, oriented so that the black and white stripes will go across the beam and block it (i.e., in the plane perpendicular to the laser beam). Make sure that the photogate starts out unblocked, so you are holding it high enough.

Press "Start Collection," wait a second for it to register, and when it actually begins collecting data, drop the fence through. Make sure the fence drops straight through and does not rotate (be careful how you drop it), and also that it does not hit the photogate on the way down.

Once it is through, press "Stop Collection." You should see some data and three plots: a position vs. time plot, a velocity vs. time plot, and an acceleration vs. time plot, all with distance units of "segments" (pairs of black/white stripes).

Look at these plots. Do they look like what you expect?³

If there is a kink in the plot somewhere (it does not look how you expect), if it hit the photogate, or if it rotated significantly as it dropped, take the data again (click "Start Collection" and drop it again). Also do so if you have fewer than three total velocity measurements (look to the table on the left to see how many data points you have).

If the data looks OK, then make a quick sketch of what they look like on the provided sketching paper. (You may want to take a screenshot for later reference as well.)

Fit a best fit line to your velocity vs. time plot as follows: highlight the data on the plot in the region where it looks like a straight line. (I.e., if it dropped smoothly, all of your data; if it bounced back in sight of the photogate, only the data before the bounce). Click "Analyze->Linear Fit" and it will output a fit with a slope. Record the slope of this line, and then click the "x" of the little "fit" box to close it.

Repeat the process (take data, check that it looks good, fit) for four more drops. (No need to sketch again, though.)

Part II: Measuring \(g\) Using Drops from Varying Height

Now, we will take a different set of measurements. We will hold the striped plastic some distance above the photogate, drop it, and look at the first velocity measured vs. height above the photogate dropped.

Begin by holding the plastic such that the bottom of the lowest black segment is about 2cm above the top of the photogate. Record this distance (as best you can measure it) to be the height \(h\).⁴

Take your uncertainty in height to be 2mm, which is dominated by the uncertainty in your ability to hold it at exactly 2cm, unless you think you did better than that, in which case you are welcome to make your own assessment.

As before, click "Start Collection," wait a second, and drop the fence. Take note of the first velocity the program records (the first measurement listed on the data table at left), and record it.

Repeat dropping from higher distances - 4cm, 6cm, etc. up to 10cm, noting the first velocity measured each time.

Part I: Measuring \(g\) Using a Velocity Vs. Time Graph

Take your five slopes, take an average using equation (2) from the Guide to Uncertainty Propagation & Error Analysis and calculate the uncertainty in this quantity using equation (3) from the same document.

As the slope of a velocity vs. time graph, the quantity measured was acceleration, which should be acceleration due to gravity. The units begin are a little wonky right now, though - "segments per second squared."

Let's fix that. First, divide the length of all the segments \(D\) by the number of segments \(N\) to get the length a single segment \(d\). Additionally, propagate uncertainty: divide the uncertainty in \(D\) by \(N\) to get the uncertainty in \(d\), following formula (7).

Then, to convert our measurement of \(g\), we just take the measurement in segments per second squared, and multiply by \(d\), the physical distance per segment. Propagate uncertainty using formula (9).

Finally, state whether this value of \(g\) agrees with the accepted value of \(9.81\)m/s\(^2\).

Part II: Measuring \(g\) Using Drops from Varying Height

First, convert your measurements of \(v\) to physical units, following the same method as for \(g\): multiply by \(d\). Propagate uncertainty, this time using formula (7), since \(v\) doesn't have uncertainty.

From there, calculate \(v^2\) and propagate uncertainty using error analysis equation (11).

Make a plot of \(v^2\) vs. \(h\), with appropriate error bars; be sure to allow for an intercept.¹ Using equation \eqref{vsq}, we can observe that the slope of this plot should be \(2g\).

Therefore, derive a measurement of \(g\) from the slope and propagate uncertainties using error analysis equation (7).

Finally, state whether this value of \(g\) agrees with the accepted value of \(9.81\)m/s\(^2\).

Your TA will ask you to answer some of the following questions (they will tell you which ones to answer):

Experimental questions:

1. In this lab, we tried to release the ruler from a stationary state. However, it may be the case that our hand was moving slightly. If we gave our ruler some initial velocity (which may vary from drop to drop), would this impact our results from part I? From part II? What does this say about the reliability of our results for each part?
2. Suppose that when you measured \(D\), you measured the fence at a slight angle, rather than straight across. (If you wanted to exaggerate this effect, suppose you measured the length from one corner to the opposite corner.) How would this affect your final measurement of \(g\) (for each part) - would you overestimate \(g\), underestimate it, or neither? Explain your answer.
3. Take the error in the above question. Suppose that the fence was off by one degree from straight. Quantitatively, what would be the relative error induced in our measurement of \(D\) (and thus \(d\), and thus \(g\))?
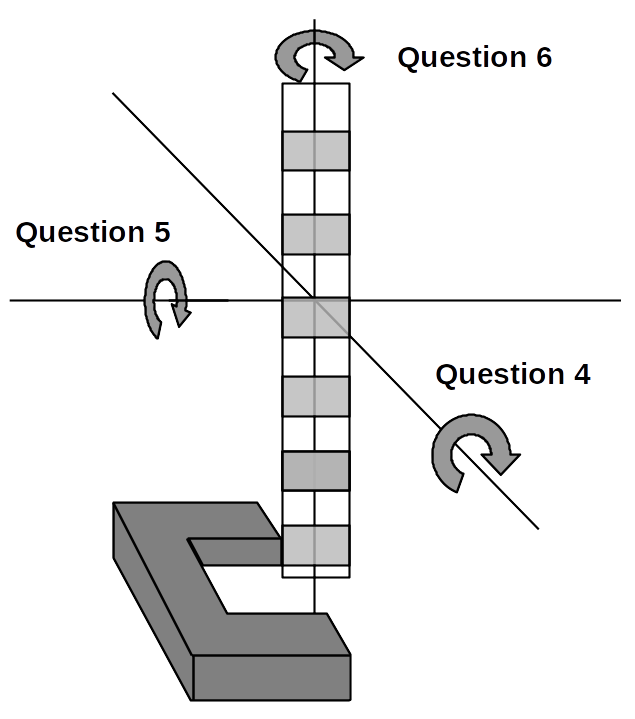
4. Suppose that when you dropped the fence, it was rotated slightly from vertical in the plane of the fence (about the z-axis, such that the "front view" of the fence was at an angle, but the "side view" was straight). How would this affect your final measurement of \(g\) (for each part) - would you overestimate \(g\), underestimate it, or neither? Explain your answer.
5. Suppose that when you dropped the fence, it was rotated slightly from vertical out of the plane of the fence (about the x-axis, such that the "side view" of the fence now had the fence at an angle, but the "front view" was straight). How would this affect your final measurement of \(g\) (for each part) - would you overestimate \(g\), underestimate it, or neither? Explain your answer. (Note: "air resistance" is not what we are looking for here.)
6. Suppose that when you dropped the fence, it was rotated slightly around the vertical axis (about the y-axis, such that it's still vertical, but not perpendicular to the photogate beam). How would this affect your final measurement of \(g\) (for each part) - would you overestimate \(g\), underestimate it, or neither? Explain your answer. (Assume that it is not rotated so much that "not seeing the ruler" becomes an issue - just a little bit.)

Theoretical questions:

1. Think carefully about what the software is actually doing: it is measuring the time when each segment totally passes through the photogate> This gives it times at which the fence has travelled certain distances (numbers of segments). How can it take these numbers and convert them into velocity and acceleration measurements? (Are they really the instantaneous velocity and acceleration measurements?)²

For further thought:

1. When we propagate error from \(D\) into \(d\), we are implicitly assuming that the measurement uncertainty is more important than the actual variation in width from stripe to stripe. If the variation in width were far larger, then we should instead be treating our measurement of \(D\) as the sum of the different widths, and the uncertainty in any particular width would be calculated according to error analysis equation (4), which amounts to dividing \(D\) by \(\sqrt{N-1}\) instead of \(N\). (In other language, we are assuming that our errors in measuring the different segments are correlated.) Based on your looking at the strip, is this justified?²

Guide to Uncertainty Propagation & Error Analysis (Quick Reference)

PHY121/122 Plotting Tool

Photogate, LabPro and LoggerPro

Kinematic Plot Sketching Paper